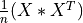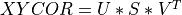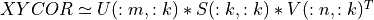MODULE Mul_Stat_Procedures¶

Module Mul_Stat_Procedures exports subroutines and functions for multivariate statistical computations. More specifically, routines for performing correlation/regression analysis, Principal Component Analysis (e.g., Empirical Orthogonal analysis in climate research), Maximum Correlation Analysis (MCA) on datasets with or without missing values are included in this module. For an introduction on these different methods, see for example [Jolliffe:2002] [Jackson:2003] [vonStorch_Zwiers:2002] [Bretherton_etal:1992]. In addition, a large variety of orthogonal rotation methods of a partial PCA model are also provided to allow a better and accurate exploration of the main spatial patterns and/or low- or high frequency modes structuring huge multivariate geophysical datasets [Jolliffe:2002] [Jackson:2003] [Jennrich:1970] [Clarkson_Jennrich:1988] [Arbuckle_Friendly:1977] [Wills_etal:2018].

Please note that routines provided in this module apply only to real data of kind stnd. The real kind type stnd is defined in module Select_Parameters.

In order to use one of these routines, you must include an appropriate use Mul_Stat_Procedures or use Statpack statement in your Fortran program, like:

use Mul_Stat_Procedures, only: comp_cor

or:

use Statpack, only: comp_cor

Here is the list of the public routines exported by module Mul_Stat_Procedures:

comp_cor()¶

Purpose:

comp_cor() computes estimates of means, variances, correlation and regression coefficients from two data arrays X and Y.

comp_cor() computes the basic univariate statistics and correlation coefficients with only one pass through the data and is efficient on huge datasets.

Moreover, comp_cor() also allows out-of-core processing of the data at the user option.

For more details on correlation and regression analysis, see Chapter 8 of [vonStorch_Zwiers:2002].

Synopsis:

call comp_cor( x(:n)       , y(:n)    , first , last , xstat(:2)       , ystat(:2)    , xycor        , xyn ,                                   z=z        , prob=prob        , ndf_max=ndf_max , cortest=cortest , cov=cov )
call comp_cor( x(:m,:n)    , y(:n)    , first , last , xstat(:m,:2)    , ystat(:2)    , xycor(:m)    , xyn , dimvar=dimvar ,                   z=z(:m)    , prob=prob(:m)    , ndf_max=ndf_max , cortest=cortest , cov=cov )
call comp_cor( x(:m,:p,:n) , y(:n)    , first , last , xstat(:m,:p,:2) , ystat(:2)    , xycor(:m,:p) , xyn ,                                   z=z(:m,:p) , prob=prob(:m,:p) , ndf_max=ndf_max , cortest=cortest , cov=cov )
call comp_cor( x(:m,:n)    , y(:p,:n) , first , last , xstat(:m,:2)    , ystat(:p,:2) , xycor(:m,:p) , xyn , dimvar=dimvar , dimvary=dimvary , z=z(:m,:p) , prob=prob(:m,:p) , ndf_max=ndf_max , cortest=cortest , cov=cov )

Examples:

ex1_comp_cor.F90

ex2_comp_cor.F90

comp_cor_miss()¶

Purpose:

comp_cor_miss() computes estimates of means, variances, correlation and regression coefficients from two data arrays X and Y, possibly containing missing values.

comp_cor_miss() computes the basic univariate statistics and correlation coefficients with only one pass through the data and is efficient on huge datasets.

The means and standard-deviations of X and Y are computed from all valid data. The correlation coefficients are based on these univariate statistics and on all valid pairs of observations.

Moreover, comp_cor_miss() also allows out-of-core processing of the data at the user option.

For more details on correlation and regression analysis, see Chapter 8 of [vonStorch_Zwiers:2002].

Synopsis:

call comp_cor_miss( x(:n)       , y(:n)    , first , last , xstat(:4)       , ystat(:4)    , xycor(:4)       , xymiss ,                                   z=z        , prob=prob        , ndf_max=ndf_max , cov=cov )
call comp_cor_miss( x(:m,:n)    , y(:n)    , first , last , xstat(:m,:4)    , ystat(:4)    , xycor(:m,:4)    , xymiss , dimvar=dimvar ,                   z=z(:m)    , prob=prob(:m)    , ndf_max=ndf_max , cov=cov )
call comp_cor_miss( x(:m,:p,:n) , y(:n)    , first , last , xstat(:m,:p,:4) , ystat(:4)    , xycor(:m,:p,:4) , xymiss ,                                   z=z(:m,:p) , prob=prob(:m,:p) , ndf_max=ndf_max , cov=cov )
call comp_cor_miss( x(:m,:n)    , y(:p,:n) , first , last , xstat(:m,:4)    , ystat(:p,:4) , xycor(:m,:p,:4) , xymiss , dimvar=dimvar , dimvary=dimvary , z=z(:m,:p) , prob=prob(:m,:p) , ndf_max=ndf_max , cov=cov )

Examples:

ex1_comp_cor_miss.F90

ex2_comp_cor_miss.F90

comp_cor_miss2()¶

Purpose:

comp_cor_miss2() computes estimates of means, variances, correlation and regression coefficients from two data arrays X and Y, possibly containing missing values.

comp_cor_miss2() computes the basic univariate statistics and correlation coefficients with only one pass through the data and is efficient on huge datasets.

The univariate and bivariate statistics are computed from all valid pairs of observations. This differs from the method used in comp_cor_miss().

Moreover, comp_cor_miss2() also allows out-of-core processing of the data at the user option.

For more details on correlation and regression analysis, see Chapter 8 of [vonStorch_Zwiers:2002].

Synopsis:

call comp_cor_miss2( x(:n)       , y(:n) , first , last , xstat(:2)       , ystat(:2)       , xycor        , xyn        , xymiss ,                 z=z        , prob=prob        , ndf_max=ndf_max )
call comp_cor_miss2( x(:m,:n)    , y(:n) , first , last , xstat(:m,:2)    , ystat(:m,:2)    , xycor(:m)    , xyn(:m)    , xymiss , dimvar=dimvar , z=z(:m)    , prob=prob(:m)    , ndf_max=ndf_max )
call comp_cor_miss2( x(:m,:p,:n) , y(:n) , first , last , xstat(:m,:p,:2) , ystat(:m,:p,:2) , xycor(:m,:p) , xyn(:m,:p) , xymiss ,                 z=z(:m,:p) , prob=prob(:m,:p) , ndf_max=ndf_max )

Examples:

ex1_comp_cor_miss2.F90

permute_cor()¶

Purpose:

permute_cor() performs permutation tests of a correlation coefficients between two data arrays Y and X.

permute_cor() is parallelized if OpenMP is used.

For more details and algorithms see Chapter 8 of [vonStorch_Zwiers:2002] and also [Noreen:1989].

Synopsis:

call permute_cor( x(:n)    , y(:n) , xstat(:2)    , ystat(:2) , xycor     , prob ,                     nrep=nrep , initseed=initseed )
call permute_cor( x(:m,:n) , y(:n) , xstat(:m,:2) , ystat(:2) , xycor(:m) , prob(:m) , dimvar=dimvar , nrep=nrep , initseed=initseed )

Examples:

ex1_permute_cor.F90

ex2_permute_cor.F90

phase_scramble_cor()¶

Purpose:

phase_scramble_cor() performs phase-scrambled bootstrap tests of correlation coefficients between two data arrays Y and X.

phase_scramble_cor() is parallelized if OpenMP is used.

For more details and algorithms see [Theiler_etal:1992] [Ebisuzaki:1997] [Braun_Kulperger:1997] [Davison_Hinkley:1997].

Synopsis:

call phase_scramble_cor( x(:n)    , y(:n) , xstat(:2)    , ystat(:2) , xycor     , prob     ,                 nrep=nrep , method=method , norm=norm , initseed=initseed )
call phase_scramble_cor( x(:m,:n) , y(:n) , xstat(:m,:2) , ystat(:2) , xycor(:m) , prob(:m) , dimvar=dimvar , nrep=nrep , method=method , norm=norm , initseed=initseed )

Examples:

ex1_phase_scramble_cor.F90

ex2_phase_scramble_cor.F90

bootstrap_cor()¶

Purpose:

bootstrap_cor() performs moving block bootstrap tests of correlation coefficients between two data arrays Y and X.

bootstrap_cor() is parallelized if OpenMP is used.

For more details and algorithms see [Davison_Hinkley:1997].

Synopsis:

call bootstrap_cor( x(:n)    , y(:n) , xstat(:2)    , xycor(:2) , prob     ,                 nrep=nrep , initseed=initseed , periodicity=periodicity , season=season , block_size=block_size )
call bootstrap_cor( x(:m,:n) , y(:n) , xstat(:m,:2) , xycor(:m) , prob(:m) , dimvar=dimvar , nrep=nrep , initseed=initseed , periodicity=periodicity , season=season , block_size=block_size )

update_cor()¶

Purpose:

update_cor() computes sample means and corrected sums of squares and cross-products for a sample of size XYN*+*XYN2 given the means and corrected sums of squares and cross-products for two subsamples of size XYN and XYN2 as output by a call to comp_cor() when LAST = false on the two subsamples separately.

The sample means, variances and coefficient correlations for the sample of size XYN*+*XYN2 may be obtained by a call to comp_cor() with LAST = true and no observations.

One possible application of this subroutine is to parallel processing. If one has two or more processors available, the sample can be split up into smaller subsamples, and the means and corrected sums of squares and cross-products computed for each subsample independently using comp_cor(). The means and corrected sums of squares and cross-products for the original sample can then be calculated using update_cor(). The means, variances and correlation coefficients for the original sample can be computed by a final call to comp_cor() with LAST = true.

Synopsis:

call update_cor( xstat(:2)       , ystat(:2) , xycor        , xyn , xstat2(:2)       , ystat2(:2) , xycor2        , xyn2 )
call update_cor( xstat(:m,:2)    , ystat(:2) , xycor(:m)    , xyn , xstat2(:m,:2)    , ystat2(:2) , xycor2(:m)    , xyn2 )
call update_cor( xstat(:m,:p,:2) , ystat(:2) , xycor(:m,:p) , xyn , xstat2(:m,:p,:2) , ystat2(:2) , xycor2(:m,:p) , xyn2 )

update_cor_miss2()¶

Purpose:

update_cor_miss2() computes sample means and corrected sums of squares and cross-products for a sample of size XYN*+*XYN2, possibly containing missing values, given the means and corrected sums of squares and cross-products for two subsamples of size XYN and XYN2 as output by a call to comp_cor_miss2() when LAST = false on the two subsamples separately.

The sample means, variances and coefficient correlations for the sample of size XYN*+*XYN2 may be obtained by a call to comp_cor() with LAST = true and no observations.

One possible application of this subroutine is to parallel processing. If one has two or more processors available, the sample can be split up into smaller subsamples, and the means and corrected sums of squares and cross-products computed for each subsample independently using comp_cor_miss2(). The means and corrected sums of squares and cross-products for the original sample can then be calculated using update_cor_miss2(). The means, variances and correlation coefficients for the original sample can be computed by a final call to comp_cor_miss2() with LAST = true.

Synopsis:

call update_cor_miss2      ( xstat(:2)       , ystat(:2)       , xycor        , xyn        , xstat2(:2)       , ystat2(:2)       , xycor2        , xyn2        )
call update_cor_miss2( xstat(:m,:2)    , ystat(:m,:2)    , xycor(:m)    , xyn(:m)    , xstat2(:m,:2)    , ystat2(:m,:2)    , xycor2(:m)    , xyn2(:m)    )
call update_cor_miss2( xstat(:m,:p,:2) , ystat(:m,:p,:2) , xycor(:m,:p) , xyn(:m,:p) , xstat2(:m,:p,:2) , ystat2(:m,:p,:2) , xycor2(:m,:p) , xyn2(:m,:p) )

comp_cormat()¶

Purpose:

comp_cormat() computes estimates of means and variance-covariance or correlation matrix (eventually in packed form in the output array argument XCORP) from a data matrix X.

comp_cormat() computes the means and correlation matrix with only one pass through the data and is efficient on huge datasets.

Moreover, comp_cormat() also allows out-of-core processing of the data at the user option.

Synopsis:

call comp_cormat( x(:m,:n) , first , last , xmean(:m) , xcor(:m,:m)         , xn , dimvar=dimvar , xstd=xstd(:m) , cov=cov , fill=fill , failure=failure )
call comp_cormat( x(:m,:n) , first , last , xmean(:m) , xcorp(:(m*(m+1))/2) , xn , dimvar=dimvar , xstd=xstd(:m) , cov=cov ,             failure=failure )

Examples:

ex1_comp_cormat.F90

ex2_comp_cormat.F90

comp_cormat_miss()¶

Purpose:

comp_cormat_miss() computes estimates of means and variance-covariance or correlation matrix (eventually in packed form in the output array argument XCORP) from a data matrix X, possibly containing missing values.

The means and standard-deviations of the data matrix X are computed from all valid data. The correlation coefficients are based on these univariate statistics and on all valid pairs of observations.

comp_cormat_miss() computes the means and correlation matrix with only one pass through the data and is efficient on huge datasets.

Moreover, comp_cormat_miss() also allows out-of-core processing of the data at the user option.

Synopsis:

call comp_cormat_miss( x(:m,:n) , first , last , xmean(:m,:2) , xcor(:m,:m)         , xn(:(m*(m+1))/2,:3) , xmiss , dimvar=dimvar , xstd=xstd(:m) , cov=cov , fill=fill , failure=failure )
call comp_cormat_miss( x(:m,:n) , first , last , xmean(:m,:2) , xcorp(:(m*(m+1))/2) , xn(:(m*(m+1))/2,:3) , xmiss , dimvar=dimvar , xstd=xstd(:m) , cov=cov ,             failure=failure )

Examples:

ex1_comp_cormat_miss.F90

ex2_comp_cormat_miss.F90

comp_eof()¶

Purpose:

comp_eof() computes estimates of Empirical Orthogonal Functions (e.g. EOF, also known as Principal Component Analysis) from a data matrix X [vonStorch_Zwiers:2002] [Jolliffe:2002] [Jackson:2003] .

comp_eof() computes the Empirical Orthogonal Functions with only one pass through the data and allows out-of-core processing at the user option.

The eigenvectors of the covariance or correlation matrix are computed with the eig_cmp2() subroutine in module EIG_Procedures.

Finally, comp_eof() may be used in a call with no observations (e.g. with size(X,3-DIMVAR) = 0) in order to finish the computations with LAST = true when the total number of observations is unknown at the beginning of the computations.

Synopsis:

call comp_eof( x(:m,:n) , first , last , xeigval(:m) , xeigvec(:m,:m) , xn , failure , dimvar=dimvar , cov=cov , sort=sort , maxiter=maxiter , xmean=xmean(:m) , xstd=xstd(:m) , xeigvar=xeigvar(:m) , xcorp=xcorp(:(m*(m+1))/2) )

Examples:

ex1_comp_eof.F90

ex1_comp_ortho_rot_eof.F90

ex1_comp_filt_rot_pc.F90

ex1_comp_lfc_rot_pc.F90

ex1_comp_smooth_rot_pc.F90

comp_eof2()¶

Purpose:

comp_eof2() computes estimates of Empirical Orthogonal Functions (e.g. EOF, also known as Principal Component Analysis) from a data matrix X [vonStorch_Zwiers:2002].

comp_eof2() computes the Empirical Orthogonal Functions with only one pass through the data and allows out-of-core processing at the user option.

comp_eof2() computes all the eigenvalues, and, optionally, selected eigenvectors (by inverse iteration), of the covariance (or correlation matrix) from the data matrix.

Thus, comp_eof2() must be used instead of comp_eof() if you are only interested in the first few Empirical Orthogonal Functions, which explains the larger part of the variance of the data matrix X and for the processing of huge datasets.

The eigenvalues and (selected) eigenvectors of the covariance or correlation matrix are computed with the eigval_cmp() and trid_inviter() subroutines in module EIG_Procedures.

Finally, comp_eof2() may be used in a call with no observations (e.g. with size(X,3-DIMVAR) = 0) in order to finish the computations with LAST = true when the total number of observations is unknown at the beginning of the computations.

Synopsis:

call comp_eof2( x(:m,:n) , first , last , xeigval(:m) , xcorp(:(m*(m+1))/2) , xn , failure , dimvar=dimvar , cov=cov , savecor=savecor , maxiter=maxiter , ortho=ortho , xmean=xmean(:m) , xstd=xstd(:m) , xeigvar=xeigvar(:m) , xeigvec=xeigvec(:m,:p) )

Examples:

ex1_comp_eof2.F90

comp_eof3()¶

Purpose:

comp_eof3() computes estimates of Empirical Orthogonal Functions (e.g. EOF, also known as Principal Component Analysis) from a data matrix X with n observations [vonStorch_Zwiers:2002].

comp_eof3() computes the matrix product

${1 \over n} (X^T * X)$ or ${1 \over n} (X * X^T)$

from the data matrix X, and all the eigenvalues, and selected eigenvectors (by inverse iteration), of this matrix product.

The eigenvalues and (selected) eigenvectors of the matrix product are computed with the eigval_cmp() and trid_inviter() subroutines in module EIG_Procedures.

Synopsis:

call comp_eof3( x(:m,:n) , dimvar=dimvar , failure , xcorp=xcorp(:(m*(m+1))/2) , xeigval=xeigval(:m,:2) , xeigvec=xeigvec(:m,:p) , maxiter=maxiter , ortho=ortho )

comp_eof_miss()¶

Purpose:

comp_eof_miss() computes estimates of Empirical Orthogonal Functions (e.g. EOF, also known as Principal Component Analysis) from a data matrix X, possibly containing missing values [vonStorch_Zwiers:2002].

The means and standard-deviations of the data matrix X are computed from all valid data. The covariance or correlation coefficients are based on these univariate statistics and on all valid pairs of observations. Finally, The eigenvectors and eigenvalues are estimated from these bivariate statistics.

comp_eof_miss() computes estimates of the Empirical Orthogonal Functions with only one pass through the data and allows out-of-core processing at the user option.

The eigenvectors of the covariance or correlation matrix are computed with the eig_cmp2() subroutine in module EIG_Procedures.

Finally, comp_eof_miss() may be used in a call with no observations (e.g. with size(X,3-DIMVAR) = 0) in order to finish the computations with LAST = true when the total number of observations is unknown at the beginning of the computations.

Synopsis:

call comp_eof_miss( x(:m,:n) , first , last , xeigval(:m,:2) , xeigvec(:m,:m) , xcorp(:(m*(m+1))/2,:3) , xmiss , failure , dimvar=dimvar , cov=cov , sort=sort , maxiter=maxiter , xmean=xmean(:m) , xstd=xtsd(:m) )

comp_eof_miss2()¶

Purpose:

comp_eof_miss2() computes estimates of Empirical Orthogonal Functions (e.g. EOF, also known as Principal Component Analysis) from a data matrix X, possibly containing missing values [vonStorch_Zwiers:2002].

The means and standard-deviations of the data matrix X are computed from all valid data. The covariance or correlation coefficients are based on these univariate statistics and on all valid pairs of observations. Finally, The eigenvectors and eigenvalues are estimated from these bivariate statistics.

comp_eof_miss2() computes the Empirical Orthogonal Functions with only one pass through the data and allows out-of-core processing at the user option.

comp_eof_miss2() computes all the eigenvalues, and, optionally, selected eigenvectors (by inverse iteration), of the covariance (or correlation matrix) from the data matrix.

Thus, comp_eof_miss2() must be used instead of comp_eof_miss() if you are only interested in the first few Empirical Orthogonal Functions, which explains the larger part of the variance of the data matrix X and for the processing of huge datasets.

The eigenvalues and (selected) eigenvectors of the covariance or correlation matrix are computed with the eigval_cmp() and trid_inviter() subroutines in module EIG_Procedures.

Finally, comp_eof_miss2() may be used in a call with no observations (e.g. with size(X,3-DIMVAR) = 0) in order to finish the computations with LAST = true when the total number of observations is unknown at the beginning of the computations.

Synopsis:

call comp_eof_miss2( x(:m,:n) , first , last , xeigval(:m,:2) , xcorp(:(m*(m+1))/2,:4) , xmiss , failure , dimvar=dimvar , cov=cov , maxiter=maxiter , ortho=ortho , xmean=xmean(:m) , xstd=xtsd(:m) , xeigvec=xeigvec(:m,:p) )

comp_eof_miss3()¶

Purpose:

comp_eof_miss3() computes estimates of Empirical Orthogonal Functions (e.g. EOF, also known as Principal Component Analysis) from a data matrix X with n observations, but possibly containing missing values [vonStorch_Zwiers:2002].

comp_eof_miss3() computes an estimate of the matrix product

${1 \over n} (X^T * X)$ or ${1 \over n} (X * X^T)$

from the data matrix X, the associated matrix of incidence values, and all the eigenvalues, and selected eigenvectors (by inverse iteration), of this matrix product.

The estimate of the above matrix product is computed from all valid pairs of observations. The eigenvectors and eigenvalues are computed from these bivariate statistics.

The eigenvalues and, optionally, (selected) eigenvectors of the matrix product are computed with the eigval_cmp() and trid_inviter() subroutines in module EIG_Procedures.

Synopsis:

call comp_eof_miss3( x(:m,:n) , xmiss , dimvar , failure , xcorp=xcorp(:(m*(m+1))/2) , xincp=xincp(:(m*(m+1))/2) , xeigval=xeigval(:m,:2) , xeigvec==xeigvec(:m,:p) , maxiter=maxiter , ortho=ortho )

comp_pc_eof()¶

Purpose:

comp_pc_eof() computes estimates of Principal Components (PC) from a data matrix and a set of eigenvectors derived from an EOF or PCA analysis.

If unnormalized PCs are desired, you must use argument XSINGVAL with all values set to one; however, in this case, do not use the optional argument XPCCOR, which will contain incorrect statistics if argument XSINGVAL is set to one.

Synopsis:

call comp_pc_eof( x(:m,:n) , xeigvec(:m,:p) , xsingval(:p) , xpc(:n,:p) , dimvar=dimvar , xmean=xmean(:m) , xstd=xtsd(:m) , xpccor=xpccor(:m,:p) )

Examples:

ex1_comp_eof.F90

ex1_comp_eof2.F90

ex1_comp_ortho_rot_eof.F90

ex1_comp_filt_rot_pc.F90

ex1_comp_lfc_rot_pc.F90

ex1_comp_smooth_rot_pc.F90

comp_ortho_rot_eof()¶

Purpose:

comp_ortho_rot_eof() performs an orthogonal rotation of a (partial) EOF model (e.g., a factor loading matrix) using a generalized orthomax criterion, including quartimax, varimax and equamax rotation methods.

For more details, see [Jennrich:1970] [Clarkson_Jennrich:1988] or [Jackson:2003].

Synopsis:

call comp_ortho_rot_eof( fac(:nv,:nf) , rot_fac(:nv,:nf) , orot(:nf,:nf) , std_rot_fac(:nf) , failure , knorm=knorm , maxiter=maxiter , w=w , delta=delta )

Examples:

ex1_comp_ortho_rot_eof.F90

comp_smooth_rot_pc()¶

Purpose:

comp_smooth_rot_pc() performs an orthogonal rotation of a (partial) EOF model (e.g., the standardized Principal Component time series) by minimizing a smoothness criterion.

For more details, see [Arbuckle_Friendly:1977] [Jolliffe:2002].

Synopsis:

call comp_smooth_rot_pc( pc(:nobs,:nf) , std_pc(:nf) , rot_pc(:nobs,:nf) , orot(:nf,:nf) , std_rot_pc(:nf) , failure , maxiter=maxiter , d=d , smooth=smooth )

Examples:

ex1_comp_smooth_rot_pc.F90

comp_lfc_rot_pc()¶

Purpose:

comp_lfc_rot_pc() performs an orthogonal rotation of a (partial) EOF model (e.g., the standardized Principal Component time series) towards low-frequency or high-frequency components using the eigenvectors of the covariance matrix between the standardized Principal Component time series filtered with a LOESS smoother.

For more details on this new orthogonal rotation method, see [Wills_etal:2018]. For information on the LOESS smoother used here for estimating the orthogonal rotation matrix applied to the standardized Principal Component time series, see [Cleveland:1979] [Cleveland_Devlin:1988] and the manual of the Time_Series_Procedures module.

Synopsis:

call comp_lfc_rot_pc( pc(:nobs,:nf) , std_pc(:nf) , nt , rot_pc(:nobs,:nf) , orot(:nf,:nf) , std_rot_pc(:nf) , failure , maxiter=maxiter , itdeg=itdeg , ntjump=ntjump , residual=residual , smooth=smooth(:nf) )

Examples:

ex1_comp_lfc_rot_pc.F90

comp_filt_rot_pc()¶

Purpose:

comp_filt_rot_pc() performs an orthogonal rotation of a (partial) EOF model (e.g., the standardized Principal Component time series) towards low-frequency, high-frequency or band-pass components using the eigenvectors of the covariance matrix between the standardized Principal Component time series filtered with a windowed FFT filter.

For more details on this new orthogonal rotation method, see [Wills_etal:2018]. For information on the windowed FFT filter used here for estimating the orthogonal rotation matrix applied to the standardized Principal Component time series, see [Iacobucci_Noullez:2005] and the manual of the Time_Series_Procedures module.

Synopsis:

call comp_filt_rot_pc( pc(:nobs,:nf) , std_pc(:nf) , pl , ph , rot_pc(:nobs,:nf) , orot(:nf,:nf) , std_rot_pc(:nf) , failure , maxiter=maxiter , trend=trend , win=win , smooth=smooth(:nf) )

Examples:

ex1_comp_filt_rot_pc.F90

comp_mca()¶

Purpose:

comp_mca() performs a Maximum Covariance Analysis (MCA) or canonical covariance analysis between two data matrices X and Y [Bretherton_etal:1992] [Bjornsson_Venegas:1997].

comp_mca() computes the Singular Value Decomposition (SVD) of the m-by-n correlation (or covariance) matrix XYCOR between two data matrices X and Y. This SVD is written

$XYCOR = U * S * V^T$

where S is a min(m,n)-by-min(m,n) diagonal matrix, U is a m-by-min(m,n) orthogonal matrix, and V is a n-by-min(m,n) orthogonal matrix. The diagonal elements of S are the singular values of XYCOR, they are real and non-negative. The columns of U and V are, respectively, the left and right singular vectors of XYCOR.

The subroutine computes the basic univariate statistics and the correlation (or covariance) matrix with only one pass through the data and allows out-of-core processing for the computation of the correlation (or covariance) matrix at the user option.

The routine returns the singular values, the left and, optionally, the right singular vectors of the correlation (or covariance) matrix XYCOR between the two data matrices X and Y.

The singular values and singular vectors of the covariance or correlation matrix are computed with the bd_cmp(), ortho_gen_bd() (or ortho_gen_q_bd()) and bd_svd() subroutines in module SVD_Procedures.

Finally, comp_mca() may be used in a call with no observations (e.g. with size(X,3-DIMVARX) = 0) in order to finish the computations with LAST = true, when the total number of observations is unknown at the beginning of the computations.

Synopsis:

call comp_mca( x(:m,:n) , y(:p,:n) , first , last , xstat(:m,:2) , ystat(:p,:2) , xysingval(:min(m,p)) , xsingvec(:m,:p) , failure , dimvarx=dimvarx , dimvary=dimvary , cov=cov , sort=sort , maxiter=maxiter , ysingvec=ysingvec(:p,:min(m,p)) , xysingvar=xysingvar(:min(m,p)) , xycor=xycor(:m,:p) )

Examples:

ex1_comp_mca.F90

comp_mca2()¶

Purpose:

comp_mca2() performs a Maximum Covariance Analysis (MCA) or canonical covariance analysis between two data matrices X and Y [Bretherton_etal:1992] [Bjornsson_Venegas:1997].

comp_mca2() computes a partial Singular Value Decomposition (SVD) of the m-by-n correlation (or covariance) matrix XYCOR between two data matrices X and Y. This partial SVD is written

$XYCOR \simeq U(:m,:k) * S(:k,:k) * V(:n,:k)^T$

where S is a k-by-k diagonal matrix, U is a m-by-k orthogonal matrix, and V is a n-by-k orthogonal matrix. The diagonal elements of S(:k,:k) are the largest singular values of XYCOR, they are real and non-negative. The columns of U(:m,:k) and V(:n,:k) are, respectively, the associated left and right singular vectors of XYCOR.

The subroutine computes the basic univariate statistics and the correlation (or covariance) matrix with only one pass through the data and allows out-of-core processing for the computation of the correlation (or covariance) matrix at the user option.

The routine returns all the singular values and, optionally, selected left and right singular vectors of the correlation (or covariance) matrix XYCOR between the two data matrices X and Y.

Thus, comp_mca2() must be used instead of comp_mca() if you are only interested in the first few singular triplets of XYCOR, which explains the larger part of the covariance or correlation between the data matrices X and Y, and for the processing of huge datasets.

The singular values and, optionally, selected singular vectors of the covariance or correlation matrix are computed (by inverse iteration) with the svd_cmp() and bd_inviter2() subroutines in module SVD_Procedures.

Finally, comp_mca2() may be used in a call with no observations (e.g. with size(X,3-DIMVARX) = 0) in order to finish the computations with LAST = true, when the total number of observations is unknown at the beginning of the computations.

Synopsis:

call comp_mca2( x(:m,:n) , y(:p,:n) , first , last , xstat(:m,:2) , ystat(:p,:2) , xysingval(:min(m,p)) , xycor(:m,:p) , failure , dimvarx=dimvarx , dimvary=dimvary , cov=cov , savecor=savecor  , maxiter=maxiter , ortho=ortho , xysingvar=xysingvar(:min(m,p)) , xysingvec=xysingvec(:m+p,:) )

Examples:

ex1_comp_mca2.F90

comp_mca_miss()¶

Purpose:

comp_mca_miss() performs a Maximum Covariance Analysis (MCA) or canonical covariance analysis between two data matrices X and Y, possibly containing missing values [Bretherton_etal:1992] [Bjornsson_Venegas:1997].

comp_mca_miss() computes the Singular Value Decomposition (SVD) of an estimate of the m-by-n correlation (or covariance) matrix XYCOR between two data matrices X and Y, possibly containing missing values. This SVD is written

$XYCOR = U * S * V^T$

where S is a min(m,n)-by-min(m,n) diagonal matrix, U is a m-by-min(m,n) orthogonal matrix, and V is a n-by-min(m,n) orthogonal matrix. The diagonal elements of S are the singular values of XYCOR, they are real and non-negative. The columns of U and V are, respectively, the left and right singular vectors of the estimate of XYCOR.

The subroutine computes the basic univariate statistics and the correlation (or covariance) matrix with only one pass through the data and allows out-of-core processing for the computation of the correlation (or covariance) matrix at the user option.

The means and standard-deviations of X and Y are computed from all valid data. The correlation (or covariance) coefficients are based on these univariate statistics and on all valid pairs of observations. The singular vectors and singular values are computed from these bivariate statistics.

The routine returns the singular values, the left and, optionally, the right singular vectors of the estimate of the correlation (or covariance) matrix XYCOR between the two data matrices X and Y.

The singular values and singular vectors of the covariance or correlation matrix are computed with the bd_cmp(), ortho_gen_bd() (or ortho_gen_q_bd()) and bd_svd() subroutines in module SVD_Procedures.

Finally, comp_mca_miss() may be used in a call with no observations (e.g. with size(X,3-DIMVARX) = 0) in order to finish the computations with LAST = true, when the total number of observations is unknown at the beginning of the computations.

Synopsis:

call comp_mca_miss( x(:m,:n) , y(:p,:n) , first , last , xstat(:m,:4) , ystat(:p,:4) , xycor(:m,:p,:4) , xymiss , failure , dimvarx=dimvarx , dimvary=dimvary , cov=cov , sort=sort , maxiter=maxiter , xysingval=xysingval(:min(m,p)) , xysingvar=xysingvar(:min(m,p)) , ysingvec=ysingvec(:p,:min(m,p)) )

comp_mca_miss2()¶

Purpose:

comp_mca_miss2() performs a Maximum Covariance Analysis (MCA) or canonical covariance analysis between two data matrices X and Y, possibly containing missing values [Bretherton_etal:1992] [Bjornsson_Venegas:1997].

comp_mca_miss2() computes a partial Singular Value Decomposition (SVD) of an estimate of the m-by-n correlation (or covariance) matrix XYCOR between two data matrices X and Y, possibly containing missing values. This partial SVD is written

$XYCOR \simeq U(:m,:k) * S(:k,:k) * V(:n,:k)^T$

where S is a k-by-k diagonal matrix, U is a m-by-k orthogonal matrix, and V is a n-by-k orthogonal matrix. The diagonal elements of S(:k,:k) are the largest singular values of XYCOR, they are real and non-negative. The columns of U(:m,:k) and V(:n,:k) are, respectively, the associated left and right singular vectors of the estimate of XYCOR.

The subroutine computes the basic univariate statistics and the correlation (or covariance) matrix with only one pass through the data and allows out-of-core processing for the computation of the correlation (or covariance) matrix at the user option.

The means and standard-deviations of X and Y are computed from all valid data. The correlation (or covariance) coefficients are based on these univariate statistics and on all valid pairs of observations. The singular vectors and singular values are computed from these bivariate statistics.

The routine returns all the singular values and, optionally, selected left and right singular vectors of the estimate of the correlation (or covariance) matrix XYCOR between the two data matrices X and Y.

Thus, comp_mca_miss2() must be used instead of comp_mca_miss() if you are only interested in the first few singular triplets of the estimate of XYCOR, which explains the larger part of the covariance or correlation between the data matrices X and Y, and for the processing of huge datasets.

The singular values and, optionally, selected singular vectors of the covariance or correlation matrix are computed (by inverse iteration) with the svd_cmp() and bd_inviter2() subroutines in module SVD_Procedures.

Finally, comp_mca_miss2() may be used in a call with no observations (e.g. with size(X,3-DIMVARX) = 0) in order to finish the computations with LAST = true, when the total number of observations is unknown at the beginning of the computations.

Synopsis:

call comp_mca_miss2( x(:m,:n) , y(:p,:n) , first , last , xstat(:m,:4) , ystatt(:p,:4) , xycor(:m,:p,:4) , xymiss , failure , dimvarx=dimvarx , dimvary=dimvary , cov=cov , xysingval=xysingval(:min(m,p)) , maxiter=maxiter , ortho=ortho , xysingvar=xysingvar(:min(m,p)) , xysingvec=xysingvec(:m+p,:) )

comp_pc_mca()¶

Purpose:

comp_pc_mca() computes estimates of Singular Variables (SV) and correlation (or covariance) fields from a data matrix X and a set of singular vectors XSINGVEC derived from the MCA analysis of the data matrix X with another matrix Y.

The subroutine computes the Singular Variables and the correlation (or covariance) fields with only one pass through the data and allows out-of-core processing at the user option.

This subroutine may be used in a call with no observations (e.g. size(X,3-DIMVAR) = size(XPC,1) = 0) in order to finish the computations with LAST = true, when the total number of observations is unknown at the beginning of the computations.

Synopsis:

call comp_pc_mca( x(:m,:n) , xsingvec(:m,:o) , first , last , xpccor(:m,:o) , pccorp(:(o*(o+1))/2) , xpc(:n,:o) , xn , dimvar=dimvar , xmean=xmean(:m) , xstd=xstd(:m) , xpcvar=xpcvar(:o)  )

Examples:

ex1_comp_mca.F90

ex1_comp_mca2.F90

comp_pc()¶

Purpose:

comp_pc() estimates of Principal Components (PC) from a data matrix X and eigenvectors or singular vectors derived from EOF or MCA analysis.

The subroutine computes the Principal Components with only one pass through the data, by projecting the observations onto the eigenvectors or singular vectors of the correlation or covariance matrix.

Synopsis:

call comp_pc( x(:m,:n) , xeigvec(:m)    , xpc(:n)    , dimvar=dimvar , xmean=xmean(:m) , xstd=xstd(:m) , xsingval=xsingval     )
call comp_pc( x(:m,:n) , xeigvec(:m,:o) , xpc(:n,:o) , dimvar=dimvar , xmean=xmean(:m) , xstd=xstd(:m) , xsingval=xsingval(:o) )

comp_pc_miss()¶

Purpose:

comp_pc_miss() estimates of Principal Components (PC) from a data matrix X and eigenvectors or singular vectors derived from EOF or MCA analysis, when X contains missing values.

The subroutine computes the Principal Components with only one pass through the data, by regressing the observations with non-missing values onto the eigenvectors or singular vectors of the correlation or covariance matrix.

When missing values are present, the Principal Components estimated by comp_pc_miss() are not necessarily uncorrelated.

Synopsis:

call comp_pc_miss( x(:m,:n) , xeigvec(:m)    , xpc(:n)    , xmiss , dimvar=dimvar , xmean=xmean(:m) , xstd=xstd(:m) , xsingval=xsingval )
call comp_pc_miss( x(:m,:n) , xeigvec(:m,:o) , xpc(:n,:o) , xmiss , dimvar=dimvar , xmean=xmean(:m) , xstd=xstd(:m) , xsingval=xsingval(:o) , tol=tol , min_norm=min_norm )

Previous topic

Next topic

MODULE Mul_Stat_Procedures¶