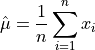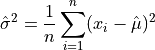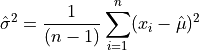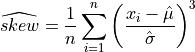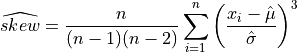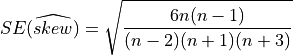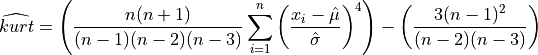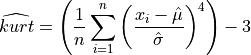MODULE Stat_Procedures¶
Module Stat_Procedures exports routines for univariate statistical computations.
All the routines in the Stat_Procedures module compute the different univariate statistics with only one pass through the data and recurrence relationships to average quantities in a stable way. Moreover, the routines can also be used to compute intermediate estimates of mean and variance on different chunks of data (eventually by different OpenMP threads), which can be merged later. This leads to high performance and out-of-core parallel methods on huge datasets. The routines may also take care of missing values in the data.
The statistical univariate procedures in the Stat_Procedures module include routines to compute the mean, variance, standard deviation, skewness, kurtosis and median on a (multi-channel) sample [vonStorch_Zwiers:2002].
The arithmetic mean, or sample mean, is denoted by 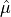 and defined as,
and defined as,
where 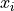 are the observations in a sample with
are the observations in a sample with n observations. For samples drawn from a gaussian
distribution the variance of 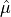 itself is
itself is 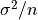 where
where 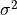 is the variance
in the parent population.
is the variance
in the parent population.
The estimated variance in a sample with n observations is denoted by 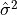 and is defined by,
and is defined by,
or
where 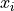 are the elements of the sample. Note that
the normalization factor of
are the elements of the sample. Note that
the normalization factor of 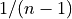 results from the derivation
of
results from the derivation
of 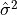 as an unbiased estimator of the population
variance
as an unbiased estimator of the population
variance 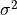 . For samples drawn from a Gaussian distribution
the variance of
. For samples drawn from a Gaussian distribution
the variance of 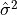 itself is
itself is 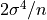 .
.
The standard deviation is just defined as the square root of the variance.
The estimated skewness computed on a sample with n observations, is defined as,
or
where 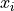 are the elements of the sample and
are the elements of the sample and 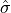 is the unbiased estimate of the
standard-deviation computed on the sample. Note that the normalization factor of
is the unbiased estimate of the
standard-deviation computed on the sample. Note that the normalization factor of 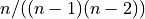 in the second
definition of
in the second
definition of 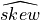 results from the derivation of
results from the derivation of 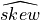 has an unbiased estimator of the
population skewness
has an unbiased estimator of the
population skewness 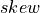 . The first biased definition is the classical formulae used in most
textbooks [vonStorch_Zwiers:2002].
The skewness measures the deviation of a distribution from symmetry. For a symmetrical distribution,
the skewness coefficient is always equal to zero, but the converse is not true.
Skewness is zero for a normal distribution. For unimodal distributions shifted to the right (left),
the skewness coefficient is positive (negative). The skewness is useful to diagnose nonlinear processes
and deviation from linearity.
. The first biased definition is the classical formulae used in most
textbooks [vonStorch_Zwiers:2002].
The skewness measures the deviation of a distribution from symmetry. For a symmetrical distribution,
the skewness coefficient is always equal to zero, but the converse is not true.
Skewness is zero for a normal distribution. For unimodal distributions shifted to the right (left),
the skewness coefficient is positive (negative). The skewness is useful to diagnose nonlinear processes
and deviation from linearity.
In order to interpret correctly the skewness computed on a sample, note that the Standard Error (SE) of the skewness coefficient
(e.g., the standard-deviation of 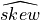 around
around 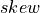 ) calculated on a sample drawn from a Gaussian
distribution is given by:
) calculated on a sample drawn from a Gaussian
distribution is given by:
This SE is not very different from 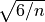 when the number of observations
when the number of observations n is sufficiently high.
Moreover, the quantity 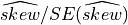 follows asymptotically a Gaussian distribution with mean
follows asymptotically a Gaussian distribution with mean 0 and variance
equal to 1 when the sample is drawn from a Gaussian distribution. With a sample of independent Gaussian observations, a value twice
the SE is thus associated with a 5% significance level suggesting a significant departure from a Gaussian distribution when the number
of observations is sufficiently large.
The estimated kurtosis, computed on a sample with n observations, is defined as,
or
The first definition is the unbiased estimator of the population kurtosis 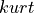 and the second
is the classical biased (but simpler) formulae used in most statistical textbooks [vonStorch_Zwiers:2002].
and the second
is the classical biased (but simpler) formulae used in most statistical textbooks [vonStorch_Zwiers:2002].
The kurtosis measures the flatness or peakedness of a distribution, i.e. how sharply peaked
a distribution is, relative to its width. The kurtosis, as defined above, is normalized to zero
for a Gaussian distribution and is always greater or equal to -2. In most cases, if
the kurtosis is greater (lower) than zero then the distribution is more peaked (flatter) than
the normal distribution with the same mean and standard-deviation.
In order to interpret correctly the kurtosis computed on a sample, note that the SE of the kurtosis coefficient calculated on a sample drawn from a Gaussian distribution is given by:
and the quantity 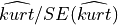 follows asymptotically a Gaussian distribution with mean
follows asymptotically a Gaussian distribution with mean 0 and variance
equal to 1 when the sample is drawn from a Gaussian distribution.
Extreme departures from the mean will cause very high (absolute) values of kurtosis. Consequently, the kurtosis coefficient can be used to detect extreme observations or outliers in a sample of observations.
In summary, if you are interested in how well a distribution can be approximated by the normal distribution, the skewness and kurtosis coefficients and their standard errors can give you some useful information.
Unbiased estimators of variance, standard-deviation, skewwness and kurtosis can be computed by the comp_unistat()
and comp_unistat_miss() subroutines. Biased estimates of variance and standard-deviation are computed by the comp_mvs()
and comp_mvs_miss() subroutines.
Finally, procedures for performing composite analysis (e.g., testing differences of means between groups of observations) are also provided in this module [Terray_etal:2003].
Please note that routines provided in this module apply only to real data of kind stnd. The real kind type stnd is defined in module Select_Parameters.
In order to use one of these routines, you must include an appropriate use Stat_Procedures or use Statpack statement
in your Fortran program, like:
use Stat_Procedures, only: comp_unistat
or:
use Statpack, only: comp_unistat
Here is the list of the public routines exported by module Stat_Procedures:
-
comp_unistat()¶
Purpose:
comp_unistat() computes estimates of univariate statistics from a data array, X. X can be a vector, a matrix or a tri- or four-dimensional array of data.
The subroutine computes the univariate statistics with only one pass through the data.
If all the data are not available at once, comp_unistat() can operate on chunks of data.
On output, the argument XSTAT will contain the following statistics:
- XSTAT(…,1) contains the mean value of the data vector.
- XSTAT(…,2) contains the variance of the data vector.
- XSTAT(…,3) contains the standard deviation of the data vector.
- XSTAT(…,4) contains the coefficient of skewness of the data vector.
- XSTAT(…,5) contains the coefficient of kurtosis of the data vector.
- XSTAT(…,6) contains the minimum of the data vector.
- XSTAT(…,7) contains the maximum of the data vector.
comp_unistat() computes unbiased estimates of variance and standard deviation.
Unbiased estimates of skewness and kurtosis are computed only if the NOBIAS logical argument is used with the value true.
Synopsis:
call comp_unistat( x(:n) , first , last , xstat(:7) , xnobs=xnobs , nobias=nobias ) call comp_unistat( x(:m,:n) , first , last , xstat(:m,:7) , xnobs=xnobs , nobias=nobias , dimvar=dimvar ) call comp_unistat( x(:m,:p,:n) , first , last , xstat(:m,:p,:7) , xnobs=xnobs , nobias=nobias ) call comp_unistat( x(:m,:p,:q,:n) , first , last , xstat(:m,:p,:7) , xnobs=xnobs , nobias=nobias ) call comp_unistat( x(:n) , first , last , xmiss , xstat(:7) , xnobs=xnobs , nobias=nobias ) call comp_unistat( x(:m,:n) , first , last , xmiss , xstat(:m,:7) , xnobs=xnobs(:m) , nobias=nobias , dimvar=dimvar ) call comp_unistat( x(:m,:p,:n) , first , last , xmiss , xstat(:m,:p,:7) , xnobs=xnobs(:m,:p) , nobias=nobias ) call comp_unistat( x(:m,:p:q,,:n) , first , last , xmiss , xstat(:m,:p,:7) , xnobs=xnobs(:m,:p) , nobias=nobias )
Examples:
-
comp_unistat_miss()¶
Purpose:
comp_unistat_miss() computes estimates of univariate statistics from a data array, X. X can be a vector, a matrix or a tri- or four-dimensional array of data, possibly containing missing values.
The subroutine computes the univariate statistics with only one pass through the data.
If all the data are not available at once, comp_unistat_miss() can operate on chunks of data.
On output, the argument XSTAT will contain the following statistics:
- XSTAT(…,1) contains the mean value of the data vector.
- XSTAT(…,2) contains the variance of the data vector.
- XSTAT(…,3) contains the standard deviation of the data vector.
- XSTAT(…,4) contains the coefficient of skewness of the data vector.
- XSTAT(…,5) contains the coefficient of kurtosis of the data vector.
- XSTAT(…,6) contains the minimum of the data vector.
- XSTAT(…,7) contains the maximum of the data vector.
comp_unistat_miss() computes unbiased estimates of variance and standard deviation.
Unbiased estimates of skewness and kurtosis are computed only if the NOBIAS logical argument is used with the value true.
Synopsis:
call comp_unistat_miss( x(:n) , first , last , xmiss , xstat(:7) , xnobs=xnobs , nobias=nobias ) call comp_unistat_miss( x(:m,:n) , first , last , xmiss , xstat(:m,:7) , xnobs=xnobs(:m) , nobias=nobias , dimvar=dimvar ) call comp_unistat_miss( x(:m,:p,:n) , first , last , xmiss , xstat(:m,:p,:7) , xnobs=xnobs(:m,:p) , nobias=nobias ) call comp_unistat_miss( x(:m,:p:q,,:n) , first , last , xmiss , xstat(:m,:p,:7) , xnobs=xnobs(:m,:p) , nobias=nobias )
-
comp_mvs()¶
Purpose:
comp_mvs() computes estimates of means, variances and standard-deviations from a data array, X. X can be a vector, a matrix or a tri- or four-dimensional array of data.
The subroutine computes the basic statistics with only one pass through the data.
If all the data are not available at once, comp_mvs() can operate on chunks of data.
comp_mvs() computes biased estimates of variance and standard deviation.
Synopsis:
call comp_mvs( x(:n) , first , last , xmean , xvar , xstd , xnobs=xnobs ) call comp_mvs( x(:m,:n) , first , last , xmean(:m) , xvar(:m) , xstd(:m) , xnobs=xnobs , dimvar=dimvar ) call comp_mvs( x(:m,:p,:n) , first , last , xmean(:m,:p) , xvar(:m,:p) , xstd(:m,:p) , xnobs=xnobs ) call comp_mvs( x(:m,:p,:q,:n) , first , last , xmean(:m,:p,:q) , xvar(:m,:p,:q) , xstd(:m,:p,:q) , xnobs=xnobs ) call comp_mvs( x(:n) , first , last , xmean , xvar , xstd , xmiss , xnobs=xnobs ) call comp_mvs( x(:m,:n) , first , last , xmean(:m) , xvar(:m) , xstd(:m) , xmiss , xnobs=xnobs(:m), dimvar=dimvar ) call comp_mvs( x(:m,:p,:n) , first , last , xmean(:m,:p) , xvar(:m,:p) , xstd(:m,:p) , xmiss , xnobs=xnobs(:m,:p) ) call comp_mvs( x(:m,:p,:q,:n) , first , last , xmean(:m,:p,:q) , xvar(:m,:p,:q) , xstd(:m,:p,:q) , xmiss , xnobs=xnobs(:m,:p,:q) )
Examples:
-
comp_mvs_miss()¶
Purpose:
comp_mvs_miss() computes estimates of means, variances and standard-deviations from a data array, X. X can be a vector, a matrix or a tri- or four-dimensional array of data, possibly containing missing values.
The subroutine computes the basic statistics with only one pass through the data.
If all the data are not available at once, comp_mvs_miss() can operate on chunks of data.
comp_mvs_miss() computes biased estimates of variance and standard deviation.
Synopsis:
call comp_mvs_miss( x(:n) , first , last , xmean , xvar , xstd , xmiss , xnobs=xnobs ) call comp_mvs_miss( x(:m,:n) , first , last , xmean(:m) , xvar(:m) , xstd(:m) , xmiss , xnobs=xnobs(:m), dimvar=dimvar ) call comp_mvs_miss( x(:m,:p,:n) , first , last , xmean(:m,:p) , xvar(:m,:p) , xstd(:m,:p) , xmiss , xnobs=xnobs(:m,:p) ) call comp_mvs_miss( x(:m,:p,:q,:n) , first , last , xmean(:m,:p,:q) , xvar(:m,:p,:q) , xstd(:m,:p,:q) , xmiss , xnobs=xnobs(:m,:p,:q) )
-
update_mvs()¶
Purpose:
update_mvs() computes sample mean and corrected sum of squares
for a sample of size XNOBS+XNOBS2 given the means and corrected sums of squares
for two subsamples of size XNOBS and XNOBS2 as output by a call to comp_mvs()
when LAST = false on the two subsamples separetely.
The sample means, standard-deviations for the sample of size XNOBS+XNOBS2
may be obtained by a final call to comp_mvs() with LAST = true and no observations.
One possible application of update_mvs() is to parallel processing. If one has two
or more processors available, the sample can be split up into smaller subsamples,
and the means and corrected sums of squares computed for each
subsample independently using comp_mvs(). The means and corrected sums of squares
for the original sample can then be calculated using update_mvs().
Finally, the means, variances and standard-deviations for the original sample can
be computed by a final call to comp_mvs() with LAST = true and no observations.
Synopsis:
call update_mvs( xmean , xvar , xnobs , xmean2 , xvar2 , xnobs2 ) call update_mvs( xmean(:m) , xvar(:m) , xnobs , xmean2(:m) , xvar2(:m) , xnobs2 ) call update_mvs( xmean(:m,:p) , xvar(:m,:p) , xnobs , xmean2(:m,:p) , xvar2(:m,:p) , xnobs2 ) call update_mvs( xmean(:m,:p,:q) , xvar(:m,:p,:q) , xnobs , xmean2(:m,:p,:q) , xvar2(:m,:p,:q) , xnobs2 )
-
comp_mvs_grp()¶
Purpose:
comp_mvs_grp() computes estimates of means, variances and standard-deviations by groups from a data array, X. X can be a vector, a matrix or a tri- or four-dimensional array of data.
The subroutine computes the basic statistics by groups with only one pass through the data.
If all the data are not available at once, comp_mvs_grp() can operate on chunks of data.
Synopsis:
call comp_mvs_grp( x(:n) , first , last , ngrp , ind(:n) , xmean_grp(:ngrp) , xstd_grp(:ngrp) , xn_grp(:ngrp) ) call comp_mvs_grp( x(:m,:n) , first , last , ngrp , ind(:n) , xmean_grp(:m,:ngrp) , xstd_grp(:m,:ngrp) , xn_grp(:ngrp), dimvar=dimvar ) call comp_mvs_grp( x(:m,:p,:n) , first , last , ngrp , ind(:n) , xmean_grp(:m,:p,:ngrp) , xstd_grp(:m,:p,:ngrp) , xn_grp(:ngrp) ) call comp_mvs_grp( x(:m,:p,:q,:n) , first , last , ngrp , ind(:n) , xmean_grp(:m,:p,:q,:ngrp) , xstd_grp(:m,:p,:q,:ngrp) , xn_grp(:ngrp) ) call comp_mvs_grp( x(:n) , first , last , ngrp , ind(:n) , xmean_grp(:ngrp) , xstd_grp(:ngrp) , xn_grp(:ngrp) , xmiss ) call comp_mvs_grp( x(:m,:n) , first , last , ngrp , ind(:n) , xmean_grp(:m,:ngrp) , xstd_grp(:m,:ngrp) , xn_grp(:m,:ngrp) , xmiss, dimvar=dimvar ) call comp_mvs_grp( x(:m,:p,:n) , first , last , ngrp , ind(:n) , xmean_grp(:m,:p,:ngrp) , xstd_grp(:m,:p,:ngrp) , xn_grp(:m,:p,:ngrp) , xmiss ) call comp_mvs_grp( x(:m,:p,:q,:n) , first , last , ngrp , ind(:n) , xmean_grp(:m,:p,:q,:ngrp) , xstd_grp(:m,:p,:q,:ngrp) , xn_grp(:m,:p,:q,:ngrp) , xmiss )
-
comp_mvs_grp_miss()¶
Purpose:
comp_mvs_grp_miss() computes estimates of means, variances and standard-deviations by groups from a data array, X. X can be a vector, a matrix or a tri- or four-dimensional array of data, possibly containing missing values.
The subroutine computes the basic statistics by groups with only one pass through the data.
If all the data are not available at once, comp_mvs_grp_miss() can operate on chunks of data.
Synopsis:
call comp_mvs_grp_miss( x(:n) , first , last , ngrp , ind(:n) , xmean_grp(:ngrp) , xstd_grp(:ngrp) , xn_grp(:ngrp) , xmiss ) call comp_mvs_grp_miss( x(:m,:n) , first , last , ngrp , ind(:n) , xmean_grp(:m,:ngrp) , xstd_grp(:m,:ngrp) , xn_grp(:m,:ngrp) , xmiss, dimvar=dimvar ) call comp_mvs_grp_miss( x(:m,:p,:n) , first , last , ngrp , ind(:n) , xmean_grp(:m,:p,:ngrp) , xstd_grp(:m,:p,:ngrp) , xn_grp(:m,:p,:ngrp) , xmiss ) call comp_mvs_grp_miss( x(:m,:p,:q,:n) , first , last , ngrp , ind(:n) , xmean_grp(:m,:p,:q,:ngrp) , xstd_grp(:m,:p,:q,:ngrp) , xn_grp(:m,:p,:q,:ngrp) , xmiss )
-
update_mvs_grp()¶
Purpose:
update_mvs_grp() computes sample mean and corrected sum of squares by groups
for a sample of size sum(XN_GRP)+sum(XN_GRP2) given the means and corrected sums of squares by groups
for two subsamples of size sum(XN_GRP) and sum(XN_GR2P), as output by a call to comp_mvs_grp()
when LAST = false on the two subsamples separetely.
The sample means, standard-deviations by groups for the sample of size sum(XN_GRP)+sum(XN_GRP2)
may be obtained by a final call to comp_mvs_grp() with LAST = true and no observations.
One possible application of update_mvs_grp() is to parallel processing. If one has two
or more processors available, the sample can be split up into smaller subsamples,
and the means and corrected sums of squares by groups computed for each
subsample independently using comp_mvs_grp(). The means and corrected sums of squares by groups
for the original sample can then be calculated using update_mvs_grp().
Finally, the means, variances and standard-deviations by groups for the original sample can
be computed by a final call to comp_mvs_grp() with LAST = true and no observations.
Synopsis:
call update_mvs_grp( xmean_grp(:n) , xstd_grp(:n) , xn_grp(:n) , xmean_grp2(:n) , xstd_grp2(:n) , xn_grp2(:n) ) call update_mvs_grp( xmean_grp(:m,:n) , xstd_grp(:m,:n) , xn_grp(:n) , xmean_grp2(:m,:n) , xstd_grp2(:m,:n) , xn_grp2(:n) ) call update_mvs_grp( xmean_grp(:m,:p,:n) , xstd_grp(:m,:p,:n) , xn_grp(:n) , xmean_grp2(:m,:p,:n) , xstd_grp2(:m,:p,:n) , xn_grp2(:n) ) call update_mvs_grp( xmean_grp(:m,:p,:q,:n) , xstd_grp(:m,:p,:q,:n) , xn_grp(:n) , xmean_grp2(:m,:p,:q,:n) , xstd_grp2(:m,:p,:q,:n) , xn_grp2(:n) ) call update_mvs_grp( xmean_grp(:m,:n) , xstd_grp(:m,:n) , xn_grp(:m,:n) , xmean_grp2(:m,:n) , xstd_grp2(:m,:n) , xn_grp2(:m,:n) ) call update_mvs_grp( xmean_grp(:m,:p,:n) , xstd_grp(:m,:p,:n) , xn_grp(:m,:p,:n) , xmean_grp2(:m,:p,:n) , xstd_grp2(:m,:p,:n) , xn_grp2(:m,:p,:n) ) call update_mvs_grp( xmean_grp(:m,:p,:q,:n) , xstd_grp(:m,:p,:q,:n) , xn_grp(:m,:p,:q,:n) , xmean_grp2(:m,:p,:q,:n) , xstd_grp2(:m,:p,:q,:n) , xn_grp2(:m,:p,:q,:n) )
-
update_mvs_grp_miss()¶
Purpose:
update_mvs_grp_miss() computes sample mean and corrected sum of squares by groups
for a sample of size sum(XN_GRP)+sum(XN_GRP2), possibly containing missing values,
given the means and corrected sums of squares by groups
for two subsamples of size sum(XN_GRP) and sum(XN_GR2P), as output by a call to comp_mvs_grp_miss()
when LAST = false on the two subsamples separetely.
The sample means, standard-deviations by groups for the sample of size sum(XN_GRP)+sum(XN_GRP2)
may be obtained by a final call to comp_mvs_grp_miss() with LAST = true and no observations.
One possible application of update_mvs_grp_miss() is to parallel processing. If one has two
or more processors available, the sample can be split up into smaller subsamples,
and the means and corrected sums of squares by groups computed for each
subsample independently using comp_mvs_grp_miss(). The means and corrected sums of squares by groups
for the original sample can then be calculated using update_mvs_grp_miss().
Finally, the means, variances and standard-deviations by groups for the original sample can
be computed by a final call to comp_mvs_grp_miss() with LAST = true and no observations.
Synopsis:
call update_mvs_grp_miss( xmean_grp(:n) , xstd_grp(:n) , xn_grp(:n) , xmean_grp2(:n) , xstd_grp2(:n) , xn_grp2(:n) ) call update_mvs_grp_miss( xmean_grp(:m,:n) , xstd_grp(:m,:n) , xn_grp(:m,:n) , xmean_grp2(:m,:n) , xstd_grp2(:m,:n) , xn_grp2(:m,:n) ) call update_mvs_grp_miss( xmean_grp(:m,:p,:n) , xstd_grp(:m,:p,:n) , xn_grp(:m,:p,:n) , xmean_grp2(:m,:p,:n) , xstd_grp2(:m,:p,:n) , xn_grp2(:m,:p,:n) ) call update_mvs_grp_miss( xmean_grp(:m,:p,:q,:n) , xstd_grp(:m,:p,:q,:n) , xn_grp(:m,:p,:q,:n) , xmean_grp2(:m,:p,:q,:n) , xstd_grp2(:m,:p,:q,:n) , xn_grp2(:m,:p,:q,:n) )
-
comp_anoma()¶
Purpose:
comp_anoma() computes anomalies (e.g., differences with the mean) or standardized anomalies from a data array X. X can be a vector, a matrix or a tridimensional array.
Synopsis:
call comp_anoma( x(:n) , xmean , xstd=xstd ) call comp_anoma( x(:m,:n) , xmean(:m) , xstd=xstd(:m) , dimvar=dimvar ) call comp_anoma( x(:m,:p,:n) , xmean(:m,:p) , xstd=xstd(:m,:p) )
-
comp_anoma_miss()¶
Purpose:
comp_anoma_miss() computes anomalies (e.g., differences with the mean) or standardized anomalies from a data array X, possibly containing missing values. X can be a vector, a matrix or a tridimensional array.
Synopsis:
call comp_anoma( x(:n) , xmiss , xmean , xstd=xstd ) call comp_anoma( x(:m,:n) , xmiss , xmean(:m) , xstd=xstd(:m) , dimvar=dimvar ) call comp_anoma( x(:m,:p,:n) , xmiss , xmean(:m,:p) , xstd=xstd(:m,:p) )
-
comp_anoma_grp()¶
Purpose:
comp_anoma_grp() computes anomalies (e.g., differences with the mean) or standardized anomalies by groups from a data array X. X can be a vector, a matrix or a tridimensional array.
Synopsis:
call comp_anoma_grp( x(:n) , ngrp , ind(:n) , xmean_grp(:ngrp) , xstd_grp=xstd_grp(:ngrp) ) call comp_anoma_grp( x(:m,:n) , ngrp , ind(:n) , xmean_grp(:m,:ngrp) , xstd_grp=xstd_grp(:m,:ngrp) , dimvar=dimvar ) call comp_anoma_grp( x(:m,:p,:n) , ngrp , ind(:n) , xmean_grp(:m,:p,:ngrp) , xstd_grp=xstd_grp(:m,:p,:ngrp) )
-
comp_anoma_grp_miss()¶
Purpose:
comp_anoma_grp_miss() computes anomalies (e.g., differences with the mean) or standardized anomalies by groups from a data array X, possibly containing missing values. X can be a vector, a matrix or a tridimensional array.
Synopsis:
call comp_anoma_grp_miss( x(:n) , ngrp , ind(:n) , xmiss , xmean_grp(:ngrp) , xstd_grp=xstd_grp(:ngrp) ) call comp_anoma_grp_miss( x(:m,:n) , ngrp , ind(:n) , xmiss , xmean_grp(:m,:ngrp) , xstd_grp=xstd_grp(:m,:ngrp) , dimvar=dimvar ) call comp_anoma_grp_miss( x(:m,:p,:n) , ngrp , ind(:n) , xmiss , xmean_grp(:m,:p,:ngrp) , xstd_grp=xstd_grp(:m,:p,:ngrp) )
-
comp_composite()¶
Purpose:
Purpose:
comp_composite() computes a composite analysis from an array of data X [Terray_etal:2003]. The array argument X can be a vector, a matrix or a tridimensional array of data and comp_composite_miss() computes all the relevant statistics with one pass through the data.
Synopsis:
call comp_composite( x(:n) , first , last , ngrp , ind(:n) , xmean , xstd , xn , xmean_grp(:ngrp) , xstd_grp(:ngrp) , xn_grp(:ngrp) , xcomp=xcomp(:ngrp) , u=u(:ngrp) , prob=prob(:ngrp) , utest=utest ) call comp_composite( x(:m,:n) , first , last , ngrp , ind(:n) , xmean(:m) , xstd(:m) , xn , xmean_grp(:m,:ngrp) , xstd_grp(:m,:ngrp) , xn_grp(:ngrp) , dimvar=dimvar , xcomp=xcomp(:m,:ngrp) , u=u(:m,:ngrp) , prob=prob(:m,:ngrp) , utest=utest ) call comp_composite( x(:m,:p,:n) , first , last , ngrp , ind(:n) , xmean(:m,:p) , xstd(:m,:p) , xn , xmean_grp(:m,:p,:ngrp) , xstd_grp(:m,:p,:ngrp) , xn_grp(:ngrp) , xcomp=xcomp(:m,:p,:ngrp) , u=u(:m,:p,:ngrp) , prob=prob(:m,:p,:ngrp) , utest=utest ) call comp_composite( x(:n) , first , last , ngrp , ind(:n) , xmean , xstd , xn , xmean_grp(:ngrp) , xstd_grp(:ngrp) , xn_grp(:ngrp) , xmiss , xcomp=xcomp(:ngrp) , u=u(:ngrp) , prob=prob(:ngrp) , utest=utest ) call comp_composite( x(:m,:n) , first , last , ngrp , ind(:n) , xmean(:m) , xstd(:m) , xn(:m) , xmean_grp(:m,:ngrp) , xstd_grp(:m,:ngrp) , xn_grp(:m,:ngrp) , xmiss , dimvar=dimvar , xcomp=xcomp(:m,:ngrp) , u=u(:m,:ngrp) , prob=prob(:m,:ngrp) , utest=utest ) call comp_composite( x(:m,:p,:n) , first , last , ngrp , ind(:n) , xmean(:m,:p) , xstd(:m,:p) , xn(:m,:p) , xmean_grp(:m,:p,:ngrp) , xstd_grp(:m,:p,:ngrp) , xn_grp(:m,:p,:ngrp) , xmiss , xcomp=xcomp(:m,:p,:ngrp) , u=u(:m,:p,:ngrp) , prob=prob(:m,:p,:ngrp) , utest=utest )
-
comp_composite_miss()¶
Purpose:
comp_composite_miss() computes a composite analysis from an array of data X [Terray_etal:2003]. The array argument X can be a vector, a matrix or a tridimensional array of data, possibly containing missing data, and comp_composite_miss() computes all the relevant statistics with one pass through the data.
Synopsis:
call comp_composite_miss( x(:n) , first , last , ngrp , ind(:n) , xmean , xstd , xn , xmean_grp(:ngrp) , xstd_grp(:ngrp) , xn_grp(:ngrp) , xmiss , xcomp=xcomp(:ngrp) , u=u(:ngrp) , prob=prob(:ngrp) , utest=utest ) call comp_composite_miss( x(:m,:n) , first , last , ngrp , ind(:n) , xmean(:m) , xstd(:m) , xn(:m) , xmean_grp(:m,:ngrp) , xstd_grp(:m,:ngrp) , xn_grp(:m,:ngrp) , xmiss , dimvar=dimvar , xcomp=xcomp(:m,:ngrp) , u=u(:m,:ngrp) , prob=prob(:m,:ngrp) , utest=utest ) call comp_composite_miss( x(:m,:p,:n) , first , last , ngrp , ind(:n) , xmean(:m,:p) , xstd(:m,:p) , xn(:m,:p) , xmean_grp(:m,:p,:ngrp) , xstd_grp(:m,:p,:ngrp) , xn_grp(:m,:p,:ngrp) , xmiss , xcomp=xcomp(:m,:p,:ngrp) , u=u(:m,:p,:ngrp) , prob=prob(:m,:p,:ngrp) , utest=utest )
-
valmed()¶
Purpose:
valmed() finds the medians of a n-element vector or of the column vectors of a matrix.
valmed() uses a modified quicksort algorithm.
Synopsis:
median = valmed( x(:n) ) median(:m) = valmed( x(:n,:m) )