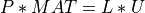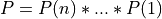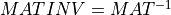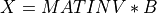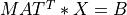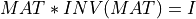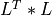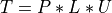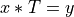MODULE Lin_Procedures

Module Lin_Procedures exports subroutines and functions for the solution of systems of linear equations, computing a triangular factorization (e.g., LU, Cholesky), computing the inverse of a square matrix or its determinant.

Routines in this module are blocked and multi-threaded versions of the standard algorithm based on the LU and Cholesky decompositions [Golub_VanLoan:1996] [Higham:2009] [Higham:2011].

A general n-by-n square matrix, MAT, has an LU decomposition into upper and lower triangular matrices:

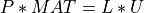
where P is a permutation matrix, L is unit lower triangular matrix and U is upper triangular matrix [Higham:2011]. This LU decomposition is also valid for singular matrices. For square full-rank matrices, this decomposition can be used to convert the linear system 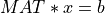into a pair of full-rank triangular systems (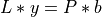, U * x = y), which can be solved by forward and backward-substitution [Higham:2011].

A symmetric, positive semidefinite square matrix MAT has a Cholesky decomposition into a product of a lower triangular matrix L and its transpose L^T [Higham:2009]:

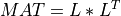
or into a product of an upper triangular matrix U and its transpose U^T:

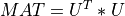
A symmetric matrix MAT is positive semidefinite if the quadratic form 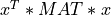is non-negative for all x. In other words, the Cholesky decomposition can only be carried out only when all the eigenvalues of the matrix are positive or null. This decomposition can be used to convert the linear system 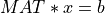into a pair of triangular systems (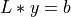, 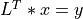), which can be solved by forward and back-substitution if all the eigenvalues of the matrix are positive [Higham:2009].

Algorithms for solving linear squares systems and for computing the inverse or the determinant of a general or positive symmetric n-by-n square matrix are based on these LU and Cholesky factorizations and the associated triangular systems.

Finally, routines for the LU factorization of a n-by-n symmetric tridiagonal matrix T as

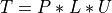
where P is a permutation matrix, L is a unit lower tridiagonal matrix with at most one non-zero sub-diagonal elements per column and U is an upper triangular matrix with at most two non-zero super-diagonal elements per column are also provided. The factorizations are obtained by Gaussian elimination with partial pivoting and implicit row scaling or with partial pivoting and row interchanges [Golub_VanLoan:1996] [Higham:2011].

If the n-by-n symmetric tridiagonal matrix T is no singular, associated linear systems can also be solved by subroutines provided in this module.

Please note that routines provided in this module apply only to real data of kind stnd. The real kind type stnd is defined in module Select_Parameters.

In order to use one of these routines, you must include an appropriate use Lin_Procedures or use Statpack statement in your Fortran program, like:

use Lin_Procedures, only: lu_cmp

or :

use Statpack, only: lu_cmp

Here is the list of the public routines exported by module Lin_Procedures:

lu_cmp()

Purpose:

lu_cmp() computes the LU decomposition with partial pivoting and implicit row scaling of a given n-by-n real matrix MAT

where P is a permutation matrix, L is a n-by-n unit lower triangular matrix and U is a n-by-n upper triangular matrix. P is a permutation matrix, stored in argument IP, such that

with P(i) is the identity with row i and IP(i) interchanged.

Synopsis:

call lu_cmp( mat(:n,:n) , ip(:n) , d1 , d2=d2 , tol=tol , small=small )

Examples:

ex1_lu_cmp.F90

ex2_lu_cmp.F90

lu_cmp2()

Purpose:

lu_cmp2() computes the LU decomposition with partial pivoting and implicit row scaling of a given n-by-n real matrix MAT

where P is a permutation matrix, L is a n-by-n unit lower triangular matrix and U is a n-by-n upper triangular matrix. P is a permutation matrix, stored in argument IP, such that

with P(i) is the identity with row i and IP(i) interchanged.

If D2 is present, lu_cmp2() computes the determinant of MAT as

determinant(MAT) = scale( D1, D2 )

If B is present, lu_cmp2() solves the system of linear equations

using the LU factorization with scaled partial pivoting of MAT. Here B is a n-vector.

If MATINV is present, lu_cmp2() computes the inverse of MAT

Synopsis:

call lu_cmp2( mat(:n,:n) , ip(:n) , d1 , d2=d2 , b=b(:n) , matinv=matinv(:n,:n) , tol=tol , small=small )

Examples:

ex1_lu_cmp2.F90

chol_cmp()

Purpose:

chol_cmp() computes the Cholesky factorization of a n-by-n real symmetric positive definite matrix MAT. The factorization has the form

, if UPPER = true or is absent,

and

, if UPPER = false,

where U is an upper triangular matrix and L is a lower triangular matrix.

Synopsis:

call chol_cmp( mat(:n,:n) , invdiag(:n) , d1 , d2=d2 , upper=upper , tol=tol )

Examples:

ex1_chol_cmp.F90

ex2_chol_cmp.F90

ex1_random_eig_pos.F90

chol_cmp2()

Purpose:

chol_cmp2() computes the Cholesky factorization of a n-by-n real symmetric positive definite matrix MAT. The factorization has the form

, if UPPER = true or is absent,

and

, if UPPER = false,

where U is an upper triangular matrix and L is a lower triangular matrix.

If D2 is present, chol_cmp2() computes the determinant of MAT as

determinant(MAT) = scale( D1, D2 )

If B is present, chol_cmp2() solves the system of linear equations

using the Cholesky factorization of MAT. Here B is a n-vector.

If MATINV is present, chol_cmp2() computes the inverse of MAT

Synopsis:

call chol_cmp2( mat(:n,:n) , invdiag(:n) , d1 , d2=d2 , b=b(:n) , matinv=matinv(:n,:n) , upper=upper , fill=fill , tol=tol )

Examples:

ex1_chol_cmp2.F90

gchol_cmp()

Purpose:

gchol_cmp() computes the Cholesky factorization of a n-by-n real symmetric positive semidefinite matrix MAT. The factorization has the form

, if UPPER = true or is absent,

and

, if UPPER = false,

where U is an upper triangular matrix and L is a lower triangular matrix.

Synopsis:

call gchol_cmp( mat(:n,:n) , invdiag(:n) , krank , d1 , d2=d2 , upper=upper , tol=tol )

Examples:

ex1_gchol_cmp.F90

ex2_gchol_cmp.F90

gchol_cmp2()

Purpose:

gchol_cmp2() computes the Cholesky factorization of a n-by-n real symmetric positive semidefinite matrix MAT. The factorization has the form

, if UPPER = true or is absent,

and

, if UPPER = false,

where U is an upper triangular matrix and L is a lower triangular matrix.

If D2 is present, gchol_cmp2() computes the determinant of MAT as

determinant(MAT) = scale( D1, D2 )

If B is present, gchol_cmp2() solves the system of linear equations

using the Cholesky factorization of MAT if B belongs to the range of MAT. Here B is a n-vector. If B does not belongs to the range of MAT, an approximate solution is computed as

where MATINV is a (generalized) inverse of MAT.

If MATINV is present, gchol_cmp2() computes a (generalized) inverse of MAT.

Synopsis:

call gchol_cmp2( mat(:n,:n) , invdiag(:n) , krank , d1 , d2=d2 , b=b(:n) , matinv=matinv(:n,:n) , upper=upper , fill=fill , tol=tol )

Examples:

ex1_gchol_cmp2.F90

lu_solve()

Purpose:

lu_solve() solves a system of linear equations

where MAT is a n-by-n coefficient matrix and B is a n-vector or a n-by-m matrix, using the LU factorization with scaled partial pivoting of MAT,

as computed by lu_cmp() or lu_cmp2().

Synopsis:

call lu_solve( mat(:n,:n) , ip(:n) , b(:n)    )
call lu_solve( mat(:n,:n) , ip(:n) , b(:n,:m) )

Examples:

ex1_lu_cmp.F90

ex2_lu_cmp.F90

lu_solve2()

Purpose:

lu_solve2() solves a system of linear equations

where MAT is a n-by-n coefficient matrix and B is a n-vector or a n-by-m matrix, using the LU factorization with scaled partial pivoting of MAT

as computed by lu_cmp() or lu_cmp2().

Synopsis:

call lu_solve2( mat(:n,:n) , ip(:n) , b(:n)    )
call lu_solve2( mat(:n,:n) , ip(:n) , b(:n,:m) )

solve_lin()

Purpose:

solve_lin() solves a system of linear equations

with a n-by-n coefficient matrix MAT. B is a n-vector or a n-by-m matrix.

The function returns the solution vector or matrix X, if the matrix MAT is not singular.

Synopsis:

x(:n)    = solve_lin( mat(:n,:n) , b(:n)    , tol=tol )
x(:n,:m) = solve_lin( mat(:n,:n) , b(:n,:m) , tol=tol )

Examples:

ex1_solve_lin.F90

ex2_solve_lin.F90

lin_lu_solve()

Purpose:

lin_lu_solve() solves a system of linear equations

with a n-by-n coefficient matrix MAT. B is a n-vector or a n-by-m matrix.

The LU decomposition with partial pivoting and implicit row scaling of the matrix MAT

where P is a permutation matrix, L is a n-by-n unit lower triangular matrix and U is a n-by-n upper triangular matrix, is used to solve the linear system.

Synopsis:

call lin_lu_solve( mat(:n,:n) , b(:n)    , failure ,            tol=tol , small=small )
call lin_lu_solve( mat(:n,:n) , b(:n,:m) , failure ,            tol=tol , small=small )
call lin_lu_solve( mat(:n,:n) , b(:n)    , failure , x(:n)    , tol=tol , small=small )
call lin_lu_solve( mat(:n,:n) , b(:n,:m) , failure , x(:n,:m) , tol=tol , small=small )

Examples:

ex1_lin_lu_solve.F90

ex2_lin_lu_solve.F90

chol_solve()

Purpose:

chol_solve() solves a system of linear equations

where MAT is a n-by-n symmetric positive definite matrix and B is a n-vector or a n-by-m matrix, using the Cholesky factorization MAT,

or

as computed by chol_cmp() or gchol_cmp().

Synopsis:

call chol_solve( mat(:n,:n) , invdiag(:n) , b(:n)    , upper=upper )
call chol_solve( mat(:n,:n) , invdiag(:n) , b(:n,:m) , upper=upper )

Examples:

ex1_chol_cmp.F90

ex2_chol_cmp.F90

ex2_gchol_cmp.F90

triang_solve()

Purpose:

triang_solve() solves a triangular system of the form

or

where MAT is a triangular matrix of order n, and B is a n-vector or a n-by-m matrix.

No test for singularity or near-singularity is included in this routine. Such tests must be performed before calling this routine.

Synopsis:

call triang_solve( mat(:n,:n) , b(:n)    ,        upper=upper , trans=trans )
call triang_solve( mat(:n,:n) , b(:n,:m) ,        upper=upper , trans=trans )
call triang_solve( mat(:n,:n) , b(:n)    , scal , upper=upper , trans=trans )
call triang_solve( mat(:n,:n) , b(:n,:m) , scal , upper=upper , trans=trans )

Examples:

ex1_h1.F90

ex1_hous1.F90

comp_inv()

Purpose:

comp_inv() computes the inverse of a real square matrix MAT.

Synopsis:

call comp_inv( mat(:n,:n) , failure ,                 tol=tol )
call comp_inv( mat(:n,:n) , failure , matinv(:n,:n) , tol=tol )

Examples:

ex1_comp_inv.F90

ex2_comp_inv.F90

inv()

Purpose:

inv() computes the inverse of a real square matrix MAT,

Synopsis:

matinv(:n,:n) = inv( mat(:n,:n) , tol=tol )

Examples:

ex1_inv.F90

comp_sym_inv()

Purpose:

comp_sym_inv() computes the inverse of a real symmetric positive definite matrix MAT using the Cholesky factorization of MAT:

or

Synopsis:

call comp_sym_inv( mat(:n,:n) , failure ,                 upper=upper , fill=fill , tol=tol )
call comp_sym_inv( mat(:n,:n) , failure , matinv(:n,:n) , upper=upper , fill=fill , tol=tol )

Examples:

ex1_comp_sym_inv.F90

sym_inv()

Purpose:

sym_inv() computes the inverse of a real symmetric positive definite matrix MAT using the Cholesky factorization MAT:

or

Synopsis:

matinv(:n,:n) = sym_inv( mat(:n,:n) , upper=upper , tol=tol )

Examples:

ex1_sym_inv.F90

comp_sym_ginv()

Purpose:

comp_sym_ginv() computes the (generalized) inverse of a real symmetric positive semidefinite matrix MAT using the Cholesky factorization MAT:

or

Synopsis:

call comp_sym_ginv( mat(:n,:n) , failure , krank ,                 upper=upper , fill=fill , tol=tol )
call comp_sym_ginv( mat(:n,:n) , failure , krank , matinv(:n,:n) , upper=upper , fill=fill , tol=tol )

Examples:

ex1_comp_sym_ginv.F90

comp_triang_inv()

Purpose:

comp_triang_inv() computes the inverse of a real upper or lower triangular matrix MAT.

Synopsis:

call comp_triang_inv( mat(:n,:n) ,                 upper=upper )
call comp_triang_inv( mat(:n,:n) , matinv(:n,:n) , upper=upper )

Examples:

ex1_comp_triang_inv.F90

ex2_comp_triang_inv.F90

comp_uut_ltl()

Purpose:

comp_uut_ltl() computes the product

or

where the triangular factor U or L is stored in the upper or lower triangular part of MAT.

Synopsis:

call comp_uut_ltl( mat(:n,:n) ,               upper=upper , fill=fill )
call comp_uut_ltl( mat(:n,:n) , prod(:n,:n) , upper=upper , fill=fill )

comp_det()

Purpose:

comp_det() computes the determinant of a real square matrix MAT

DET = determinant( MAT )

Synopsis:

call comp_det( mat(:n,:n) , det , tol=tol , man_det=man_det , exp_det=exp_det )

Examples:

ex1_comp_det.F90

det()

Purpose:

det() computes the determinant of a real square matrix MAT

DET = determinant( MAT )

Synopsis:

matdet = det( mat(:n,:n) , tol=tol )

Examples:

ex1_det.F90

sym_trid_cmp()

Purpose:

sym_trid_cmp() factorizes an n-by-n symmetric tridiagonal matrix T as

where P is a permutation matrix, L is a unit lower tridiagonal matrix with at most one non-zero sub-diagonal elements per column and U is an upper triangular matrix with at most two non-zero super-diagonal elements per column.

The factorization is obtained by Gaussian elimination with partial pivoting and implicit row scaling.

Synopsis:

call sym_trid_cmp( d(:n), e(:n), sub(:n), diag(:n), sup1(:n), sup2(:n), perm(:n), tol=tol )

sym_trid_cmp2()

Purpose:

sym_trid_cmp2() factorizes an n-by-n symmetric tridiagonal matrix T, as

where P is a permutation matrix, L is a unit lower tridiagonal matrix with at most one non-zero sub-diagonal elements per column and U is an upper triangular matrix with at most two non-zero super-diagonal elements per column.

The factorization is obtained by Gaussian elimination with partial pivoting and row interchanges.

Synopsis:

call sym_trid_cmp2( d(:n), e(:n), sub(:n), diag(:n), sup1(:n), sup2(:n), perm(:n) )

sym_trid_solve()

Purpose:

sym_trid_solve() may be used to solve the system of linear equations

where T is an n-by-n symmetric tridiagonal matrix for x, following the factorization of T by sym_trid_cmp() or sym_trid_cmp2() as

where P is a permutation matrix, L is a unit lower tridiagonal matrix with at most one non-zero sub-diagonal elements per column and U is an upper triangular matrix with at most two non-zero super-diagonal elements per column.

No test for singularity or near-singularity is included in this routine. Such tests must be performed before calling this routine.

Synopsis:

call sym_trid_solve( sub(:n), diag(:n), sup1(:n), sup2(:n), perm(:n), y(:n), scale  )
call sym_trid_solve( sub(:n), diag(:n), sup1(:n), sup2(:n), perm(:n), y(:n)         )