MODULE Giv_Procedures¶
Module Giv_Procedures exports subroutines for computing and applying Givens rotations and reflections [Golub_VanLoan:1996]. Both standard and fast Givens rotations/reflections are implemented in this module.
A Givens rotation is a rotation in the plane acting on two elements of a given vector. Givens rotations are typically used to introduce zeros in
vectors, such as during the QR decomposition of a matrix [Golub_VanLoan:1996]. In this case, it is typically desired to find scalars cs
and sn such that
where 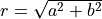 and
and 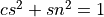 .
.
The standard Givens rotations/reflections routines in Giv_Procedures use algorithms and guidelines provided in Section 3.4 of [Anderson_Fahey:1997].
The fast Givens rotations/reflections routines in Giv_Procedures are implementations of the two-way branch algorithms (fast plane rotations with dynamic scaling to avoid overflow/underflow) described in [Anda_Park:1994].
Please note that routines provided in this module apply only to real data of kind stnd. The real kind type stnd is defined in module Select_Parameters.
In order to use one of these routines, you must include an appropriate use Giv_Procedures or use Statpack statement
in your Fortran program, like:
use Giv_Procedures, only: define_rot_givens
or :
use Statpack, only: define_rot_givens
Here is the list of the public routines exported by module Giv_Procedures:
-
define_rot_givens()¶
purpose:
define_rot_givens() generates the cosine and sine of a Givens plane rotation, so that
where 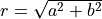 and
and 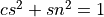 .
.
On output, the rotation is also stored in compact form in B and can be recovered by the following algorithm:
- If
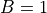 , set
, set 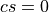 and
and 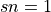
- If
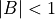 , set
, set 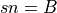 and
and 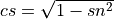
- If
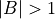 , set
, set 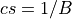 and
and 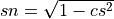
Synopsis:
call define_rot_givens( a , b , cs , sn )
-
rot_givens()¶
purpose:
rot_givens() generates and applies a Givens plane rotation to the vector (a b) or to the n-by-2 matrix [VECA VECB], so that
where 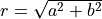 and
and 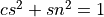 , or
, or
where:
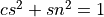 ,
,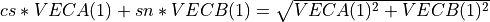 ,
,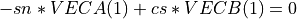 .
.
On output, the rotation is also stored in compact form in B (or VECB(1)) and can be recovered by the following algorithm:
- If
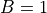 , set
, set 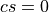 and
and 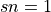
- If
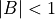 , set
, set 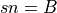 and
and 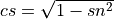
- If
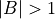 , set
, set 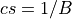 and
and 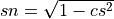
Synopsis:
call rot_givens( a , b ) call rot_givens( veca(:n) , vecb(:n) ) call rot_givens( a , b , cs , sn ) call rot_givens( veca(:n) , vecb(:n) , cs , sn )
-
apply_rot_givens()¶
purpose:
apply_rot_givens(), eventually reconstructs a Givens plane rotation, stored in compact form in B,
and applies this Givens plane rotation to the vector (c d) or to two vectors VECC and VECD.
That is, the value B allows the cosine and sine of the Givens plane rotation to be recovered by the following algorithm:
- If
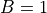 , set
, set 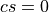 and
and 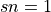
- If
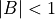 , set
, set 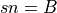 and
and 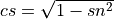
- If
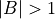 , set
, set 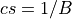 and
and 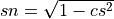
Next, the Givens plane rotation is applied to the vector (c d):
or to two vectors VECC and VECD:
where 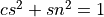 .
.
Synopsis:
call apply_rot_givens( c , d , b ) call apply_rot_givens( vecc(:n) , vecd(:n) , b ) call apply_rot_givens( c , d , cs , sn ) call apply_rot_givens( vecc(:n) , vecd(:n) , cs , sn )
-
givens_vec()¶
purpose:
givens_vec() defines and applies a Givens plane rotation to the n-by-2 matrix [VECA VECB].
The rotation is designed to annihilate the first element of VECB (e.g., VECB(1)). That is,
where:
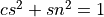 ,
,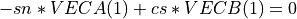 ,
,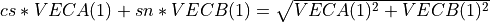 .
.
Synopsis:
call givens_vec( veca(:n) , vecb(:n) ) call givens_vec( veca(:n) , vecb(:n) , cs , sn )
-
givens_mat_left()¶
purpose:
givens_mat_left() transforms the matrix MAT to upper trapezoidal form by applying
a series of Givens plane rotations on the rows of MAT.
Synopsis:
call givens_mat_left( mat(:,:) )
Examples:
-
givens_mat_right()¶
purpose:
givens_mat_right() transforms the matrix MAT to lower trapezoidal form by applying
a series of Givens plane rotations on the columns of MAT.
Synopsis:
call givens_mat_right( mat(:,:) )
Examples:
-
givens_vec_mat_left()¶
purpose:
givens_vec_mat_left() defines and applies a series of Givens rotations on a n-vector
VEC and on the rows of a p-by-n matrix MAT.
The rotations are designed to annihilate all the elements of the first column of MAT.
Synopsis:
call givens_vec_mat_left( vec(:n) , mat(:p,:n) )
-
givens_vec_mat_right()¶
purpose:
givens_vec_mat_right() defines and applies a series of Givens rotations on a n-vector
VEC and on the columns of a p-by-n matrix MAT.
The rotations are designed to annihilate all the elements of the first row of MAT.
Synopsis:
call givens_vec_mat_right( vec(:p) , mat(:p,:n) )
-
define_rot_fastgivens()¶
purpose:
define_rot_fastgivens() generates a fast Givens plane rotation H (defined by BETA, ALPHA,
and TYPE_ROT on output) and updated scale factors (D1 and D2), which zero X2. That is,
where H is equal to
, if TYPE_ROT = 0.
, if TYPE_ROT = 1
, if TYPE_ROT = 2
, if TYPE_ROT = 3
, if TYPE_ROT = 4
On output, the arguments BETA = B and ALPHA = A and TYPE_ROT define the transformation matrix H:
Furthermore, if on input, y1 = x1*sqrt(d1) and y2 = x2*sqrt(d2), then on output, with the updated scale factors D1 and D2:
is equal to
with 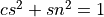 .
.
In other words, the action of H is equivalent to a standard Givens plane rotation, which zeros y2.
This subroutine is a square root free implementation of the two-way branch algorithm (fast plane rotations with dynamic scaling to avoid overflow/underflow) described in [Anda_Park:1994].
The arguments X1 and X2 are unchanged on return.
Synopsis:
call define_rot_fastgivens( x1 , x2 , d1 , d2 , beta , alpha , type_rot )
-
apply_rot_fastgivens()¶
purpose:
apply_rot_fastgivens() applies a fast Givens plane rotation H (defined by BETA, ALPHA,
and TYPE_ROT on input) to the vector (y1 y2): or to the n-by-2 matrix [VECY1 VECY2]. That is,
or
where H is a 2-by-2 matrix defined as
More precisely, H takes one of the following forms:
, if TYPE_ROT = 0.
, if TYPE_ROT = 1
, if TYPE_ROT = 2
, if TYPE_ROT = 3
, if TYPE_ROT = 4
Synopsis:
call apply_rot_fastgivens( y1, y2, beta, alpha, type_rot ) call apply_rot_fastgivens( vecy1(:n), vecy2(:n), beta, alpha, type_rot )
-
fastgivens_vec()¶
purpose:
fastgivens_vec() generates and applies a fast Givens plane rotation H to
the n-by-2 matrix [VECX1 VECX2]. The rotation is designed to zero VECX2(1).
That is,
where 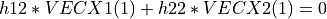 and
and H is the 2-by-2 matrix:
Furthermore, the scale factors (D1 and D2) are updated accordingly. That is, if on input:
then on output:
with 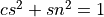 and
and 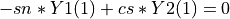 .
.
In other words, the action of H is equivalent to a standard Givens plane rotation, which zeros 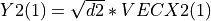 .
.
See the subroutine define_rot_fastgivens() for further details on the form of H.
Synopsis:
call fastgivens_vec( vecx1(:n) , vecx2(:n) , d1 , d2 ) call fastgivens_vec( vecx1(:n) , vecx2(:n) , d1 , d2, beta , alpha , type_rot )
-
fastgivens_mat_left()¶
purpose:
fastgivens_mat_left() reduces the matrix MAT to upper trapezoidal form by applying
a series of fast Givens plane rotations on the rows of MAT.
The (row) scale factors (MATD) are updated accordingly.
Synopsis:
call fastgivens_mat_left( mat(:p,:n), matd(:p) )
Examples:
-
fastgivens_mat_right()¶
purpose:
fastgivens_mat_right() reduces the matrix MAT to lower trapezoidal form by applying
a series of fast Givens plane rotations on the columns of MAT.
The (column) scale factors (MATD) are updated accordingly.
Synopsis:
call fastgivens_mat_right( mat(:p,:n), matd(:n) )
Examples:
-
fastgivens_vec_mat_left()¶
purpose:
fastgivens_vec_mat_left() defines and applies a series of fast Givens plane rotations on
the n-vector VEC and on the rows of a m-by-n matrix MAT.
The rotations are designed to annihilate all the elements of the first column of MAT.
The (row) scale factors (VECD and MATD) are updated accordingly.
Synopsis:
call fastgivens_vec_mat_left( vec(:n) , mat(:p,:n), vecd , matd(:p) )
-
fastgivens_vec_mat_right()¶
purpose:
fastgivens_vec_mat_right() defines and applies a series of fast Givens plane rotations on
the data:m-vector VEC and on the columns of a m-by-n matrix MAT.
The rotations are designed to annihilate all the elements of the first row of MAT.
The (column) scale factors (VECD and MATD) are updated accordingly.
Synopsis:
call fastgivens_vec_mat_right( vec(:p) , mat(:p,:n) , vecd , matd(:n) )
-
define_rot_fastgivens2()¶
purpose:
define_rot_fastgivens2() generates a fast Givens plane rotation H (defined by BETA, ALPHA,
and TYPE_ROT on output) and updated scale factors (D1 and D2) , which zero X2. That is,
where H is equal to
, if TYPE_ROT = 0.
, if TYPE_ROT = 1
, if TYPE_ROT = 2
, if TYPE_ROT = 3
, if TYPE_ROT = 4
On output, the arguments BETA = B and ALPHA = A and TYPE_ROT define the transformation matrix H:
Furthermore, if on input, y1 = x1*d1 and y2 = x2*d2, then on output, with the updated scale factors D1 and D2:
is equal to
with 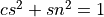 .
.
In other words, the action of H is equivalent to a standard Givens plane rotation, which zeros y2.
This subroutine is an implementation of the two-way branch algorithm (fast plane rotations with dynamic scaling to avoid overflow/underflow) described in [Anda_Park:1994].
The arguments X1 and X2 are unchanged on return.
Synopsis:
call define_rot_fastgivens2( x1 , x2 , d1 , d2 , beta , alpha , type_rot )
-
fastgivens2_vec()¶
purpose:
fastgivens2_vec() generates and applies a fast Givens plane rotation H to
the n-by-2 matrix [VECX1 VECX2]. The rotation is designed to zero VECX2(1).
That is,
where 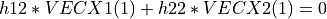 and
and H is the 2-by-2 matrix:
Furthermore, the scale factors (D1 and D2) are updated accordingly. That is, if on input:
then on output:
with 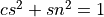 and
and 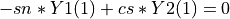 .
.
In other words, the action of H is equivalent to a standard Givens plane rotation, which zeros 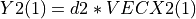 .
.
See the subroutine define_rot_fastgivens2() for further details on the form of H.
Synopsis:
call fastgivens2_vec( vecx1(:n) , vecx2(:n) , d1 , d2 ) call fastgivens2_vec( vecx1(:n) , vecx2(:n) , d1 , d2, beta , alpha , type_rot )

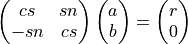
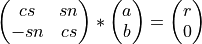
![\left(\begin{matrix} cs & sn \\ -sn & cs \end{matrix} \right) * \left[ \begin{matrix} VECA^T \\ VECB^T \end{matrix} \right] = \left[ \begin{matrix} cs*VECA^T + sn*VECB^T \\ -sn*VECA^T + cs*VECB^T \end{matrix} \right]](../_images/math/672c473d8290f57a4c2394bcc7472ec47ec18cb7.png)
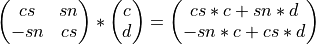
![\left(\begin{matrix} cs & sn \\ -sn & cs \end{matrix} \right) * \left[ \begin{matrix} VECC^T \\ VECD^T \end{matrix} \right] = \left[ \begin{matrix} cs*VECC^T + sn*VECD^T \\ -sn*VECC^T + cs*VECD^T \end{matrix} \right]](../_images/math/3d5571269bdb96e1a26e00a7576bd119c3b1d11c.png)
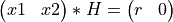
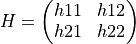
![\left(\begin{matrix} x1 & x2 \end{matrix} \right) * H * diag( \begin{matrix} \sqrt{d1} & \sqrt{d2} \end{matrix} ) = \left( \begin{matrix} [x1*h11 + x2*h21]*\sqrt{d1} & 0 \end{matrix} \right)](../_images/math/5009c03ffbbc95bc8d8e8a6bac2b12c8a644821b.png)
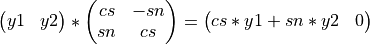
![\left(\begin{matrix} y1 & y2 \end{matrix} \right) * H = \left( \begin{matrix} [h11*y1 + h21*y2] & [h12*y1 + h22*y2] \end{matrix} \right)](../_images/math/a9ebaed5413e7076b4700a292386654896e4ffd0.png)
![[ \begin{matrix} VECY1 & VECY2 \end{matrix} ] * H = [ \begin{matrix} (h11*VECY1 + h21*VECY2) & (h12*VECY1 + h22*VECY2) \end{matrix} ]](../_images/math/cd4c6fce1259859a6000036c01abc8df4672f005.png)
![[ \begin{matrix} VECX1 & VECX2 \end{matrix} ] * H = [ \begin{matrix} (h11*VECX1 + h21*VECX2) & (h12*VECX1 + h22*VECX2) \end{matrix} ]](../_images/math/ee00e6e1a9b010d5e5c2a75a49f88c735c7388ce.png)
![[ \begin{matrix} Y1 & Y2 \end{matrix} ] = [ \begin{matrix} \sqrt{d1}*VECX1 & \sqrt{d2}*VECX2 \end{matrix} ]](../_images/math/f7219f6cf417f0048b9190d19c3a8aca6f9798a8.png)
![[ \begin{matrix} \sqrt{d1}*VECX1 & \sqrt{d2}*VECX2 \end{matrix} ] = [ \begin{matrix} Y1 & Y2 \end{matrix} ] * \left(\begin{matrix} cs & -sn \\ sn & cs \end{matrix} \right) = [ \begin{matrix} (cs*Y1 + sn*Y2) & (-sn*Y1 + cs*Y2) \end{matrix} ]](../_images/math/0e6788366a4d2c5d8012685ce99a0fb93d7e1cd3.png)
![\left(\begin{matrix} x1 & x2 \end{matrix} \right) * H * diag( \begin{matrix} d1 & d2 \end{matrix} ) = \left( \begin{matrix} [x1*h11 + x2*h21]*d1 & 0 \end{matrix} \right)](../_images/math/47cabc6410254a6a7170ac36fcaa3515b3726759.png)
![[ \begin{matrix} Y1 & Y2 \end{matrix} ] = [ \begin{matrix} d1*VECX1 & d2*VECX2 \end{matrix} ]](../_images/math/2374c5df619ad6f9762e1b6ca2f3c4ce48682a3d.png)
![[ \begin{matrix} d1*VECX1 & d2*VECX2 \end{matrix} ] = [ \begin{matrix} Y1 & Y2 \end{matrix} ] * \left(\begin{matrix} cs & -sn \\ sn & cs \end{matrix} \right) = [ \begin{matrix} (cs*Y1 + sn*Y2) & (-sn*Y1 + cs*Y2) \end{matrix} ]](../_images/math/09a2f478da03dbe12c4bbe0b118f21f0b007181f.png)