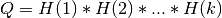MODULE QR_Procedures¶
Module QR_Procedures exports subroutines for computing QR and LQ decompositions and related factorizations or computations.
A general rectangular m-by-n matrix MAT has a QR decomposition into the product of an orthogonal
m-by-m square matrix Q (where 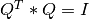 ) and a
) and a m-by-n upper-triangular
(or upper trapezoidal) matrix R [Lawson_Hanson:1974] [Golub_VanLoan:1996] [Hansen_etal:2012],
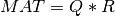
Similarly, MAT has a LQ decomposition into the product of a m-by-n lower-triangular (or lower trapezoidal)
matrix L and an orthogonal n-by-n square matrix Q (where 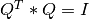 ) [Lawson_Hanson:1974]
[Golub_VanLoan:1996],
) [Lawson_Hanson:1974]
[Golub_VanLoan:1996],
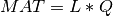
The QR decomposition can be used to convert a full rank n-by-n linear system 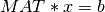 into the triangular
system
into the triangular
system 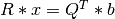 , which can be solved by back-substitution.
, which can be solved by back-substitution.
Similarly, the LQ decomposition can be used to convert a full rank n-by-n linear system 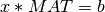 into the triangular
system
into the triangular
system 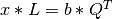 , which can also be solved by back-substitution.
, which can also be solved by back-substitution.
The QR or LQ decompositions can also be used to solve linear least squares problems, when MAT has full
rank [Lawson_Hanson:1974] [Golub_VanLoan:1996] [Hansen_etal:2012].
See the module LLSQ_Procedures for more details.
Another use of the QR or LQ decompositions is to compute an orthonormal basis for a set of vectors. The first min(m,n) columns
of Q of the QR decomposition form an orthonormal basis for the range of MAT, 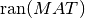 , when
, when MAT has full
rank. Similarly, the first min(m,n) rows of Q of the LQ decomposition form an orthonormal basis for the range of
MATT, when MAT has full rank.
The QR decomposition of a m-by-n matrix MAT can be extended to the rank deficient case by introducing a column
permutation P [Lawson_Hanson:1974] [Golub_VanLoan:1996] [Hansen_etal:2012],
![MAT * P = Q * R = Q * \left[ \begin{matrix} R11 & R12 \\ 0 & R22 \end{matrix} \right] \simeq \left[ \begin{matrix} R11 & R12 \\ 0 & 0 \end{matrix} \right]](../_images/math/2e28e8398fb229fa1b8b694d005d0db916df4a46.png)
where P is a permutation of the columns of In, the identity matrix of order n, R11 is a r-by-r
full rank upper triangular matrix, R12 is a r-by-n-r matrix and R22 is a (m-r)-by-(n-r) upper
triangular matrix, which is almost negligible. In other words, when MAT is rank deficient with 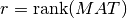 , the matrix
, the matrix R
can be partitioned into four submatrices and the dimension of R11 is equal to 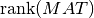 . The effective rank of
. The effective rank of MAT, r,
can be estimated by the routines provided here.
When MAT is square and of full rank (e.g. r = m = n), this decomposition can also be used to convert the linear system 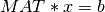 into the triangular system
into the triangular system 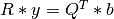 ,
, 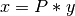 , which can be solved by back-substitution and permutation.
, which can be solved by back-substitution and permutation.
More generally, for a matrix with column rank r, The first r columns of Q form an orthonormal basis for the range of MAT
and the QR decomposition with column pivoting can be used to solve rank deficient linear least squares problems. See the module
LLSQ_Procedures for more details.
Finally, the Complete Orthogonal Decomposition (COD) of a m-by-n matrix MAT [Lawson_Hanson:1974] [Golub_VanLoan:1996]
[Hansen_etal:2012] is a generalization of the QR decomposition with column pivoting described above, given by
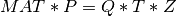
where P is a n-by-n permutation matrix, Q is a m-by-m orthogonal matrix,
Z is a n-by-n orthogonal matrix and T is a m-by-n matrix.
If MAT has full column rank, then T = R, Z = I and this reduces to the QR decomposition with column pivoting.
On the other hand, if MAT is column deficient, T has the form:
where T11 is a r-by-r upper triangular full rank matrix and r is the effective rank of MAT.
The advantage of using the complete orthogonal decomposition for rank deficient matrices is the ability to compute the minimum norm solution
to the linear least squares problem 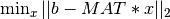 . See description of the routines in
module LLSQ_Procedures for more details.
. See description of the routines in
module LLSQ_Procedures for more details.
All these decompositions can be performed with routines available in this module. Moreover, most routines in this module are blocked and multi-threaded versions [Walker:1988] [Dongarra_etal:1989] of the standard sequential algorithms for the QR, LQ, QR with column pivoting and complete orthogonal decompositions [Lawson_Hanson:1974] [Golub_VanLoan:1996].
Please note that routines provided in this module apply only to real data types.
In order to use one of these routines, you must include an appropriate use QR_Procedures or use Statpack statement
in your Fortran program, like:
use QR_Procedures, only: lq_cmp
or :
use Statpack, only: lq_cmp
Here is the list of the public routines exported by module QR_Procedures:
-
lq_cmp()¶
Purpose:
lq_cmp() computes a LQ factorization of a real m-by-n matrix MAT :
where Q is orthogonal and L is lower trapezoidal (lower triangular if m<=n).
Synopsis:
call lq_cmp( mat(:m,:n) , diagl(:min(m,n)) , tau(:min(m,n)) , use_qr=use_qr )
Examples:
-
ortho_gen_lq()¶
Purpose:
ortho_gen_lq() generates an m-by-n real matrix with orthonormal rows, which is
defined as the first m rows of a product of k elementary reflectors of order n
as returned by lq_cmp().
Synopsis:
call ortho_gen_lq( mat(:m,:n) , tau(:p) , use_qr=use_qr )
Examples:
-
apply_q_lq()¶
Purpose:
apply_q_lq() overwrites the general real m-by-n matrix C with
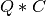 if LEFT =
if LEFT = trueand TRANS =false,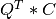 if LEFT =
if LEFT = trueand TRANS =true,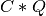 if LEFT =
if LEFT = falseand TRANS =false,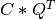 if LEFT =
if LEFT = falseand TRANS =true,
where Q is a real orthogonal matrix defined as the product of k
elementary reflectors
as returned by lq_cmp(). Q is of order m if LEFT = true and of order n
if LEFT = false.
Synopsis:
call apply_q_lq( mat(:m,:n) , tau(:p) , c(:n) , trans ) call apply_q_lq( mat(:m,:n) , tau(:p) , c(:mc,:nc) , left , trans )
-
qr_cmp()¶
Purpose:
qr_cmp() computes a QR factorization of a real m-by-n matrix MAT :
where Q is orthogonal and R is upper trapezoidal (upper triangular if m>=n).
Synopsis:
call qr_cmp( mat(:m,:n) , diagr(:p) , beta(:p) )
Examples:
-
qr_cmp2()¶
Purpose:
qr_cmp2() computes a (complete) orthogonal factorization of a real m-by-n matrix
MAT. MAT may be rank-deficient. The routine first computes a QR factorization
with column pivoting of MAT:
here P is n-by-n permutation matrix, R is an upper triangular or trapezoidal
(if n>m) matrix and Q is a m-by-m orthogonal matrix.
R can then be partitioned by defining R11 as the largest leading squared submatrix of R whose
estimated condition number, in the 1-norm, is less than 1/TOL (or such that 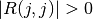 if the argument TOL is absent). The order of
if the argument TOL is absent). The order of R11, krank, is the effective rank of MAT.
This leads to the following partition of R:
where R22 can be considered to be negligible.
If TAU is present, R22 is considered to be negligible and R12 is annihilated
by orthogonal transformations from the right, arriving at the complete orthogonal factorization:
where P is a n-by-n permutation matrix, Q is a m-by-m orthogonal matrix,
Z is a n-by-n orthogonal matrix and T11 is a krank-by-krank upper
triangular matrix.
Synopsis:
call qr_cmp2( mat(:m,:n) , diagr(:min(m,n)) , beta(:min(m,n)), ip(:n) , krank , tol=tol , tau=tau(:min(m,n)) )
Examples:
-
qrfac()¶
Purpose:
qrfac() is a low level subroutine for computing a (complete) orthogonal factorization
of the array section SYST(1:m,1:n) where n <= size(SYST,2) and
m = size(SYST,1).
The routine first computes a QR factorization with column pivoting:
where P is n-by-n permutation matrix, R is an upper triangular or trapezoidal
(if n>m) matrix and Q is a m-by-m orthogonal matrix.
The orthogonal transformation Q is then applied to SYST(1:m,n+1:):
Then, the rank of SYST(1:m,1:n) is determined by finding the squared submatrix R11 of R
which is defined as the largest leading submatrix whose estimated condition
number, in the 1-norm, is less than 1/TOL or such that 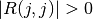 if TOL
is absent. The order of
if TOL
is absent. The order of R11, krank, is the effective rank of SYST(1:m,1:n).
This leads to the following partition of R:
where R22 can be considered to be negligible.
If MIN_NORM = true, R22 is considered to be negligible and R12 is annihilated by orthogonal
transformations from the right, arriving at the complete orthogonal factorization:
where P is a n-by-n permutation matrix, Q is a m-by-m orthogonal matrix,
Z is a n-by-n orthogonal matrix and T11 is a krank-by-krank upper
triangular matrix.
Synopsis:
call qrfac( name_proc , syst(:m,:n) , kfix , krank , min_norm, diagr(:) , beta(:) , h(:) , tol=tol , ip=ip(:) )
-
ortho_gen_qr()¶
Purpose:
ortho_gen_qr() generates an m-by-n real matrix with orthonormal columns, which is
defined as the first n columns of a product of k elementary reflectors of order m
as returned by qr_cmp() or qr_cmp2().
Synopsis:
call ortho_gen_qr( mat(:m,:n) , beta(:p) )
Examples:
-
apply_q_qr()¶
Purpose:
apply_q_qr() overwrites the general real m-by-n matrix C with
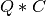 if LEFT =
if LEFT = trueand TRANS =false,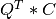 if LEFT =
if LEFT = trueand TRANS =true,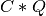 if LEFT =
if LEFT = falseand TRANS =false,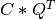 if LEFT =
if LEFT = falseand TRANS =true,
where Q is a real orthogonal matrix defined as the product of k
elementary reflectors
as returned by qr_cmp() or qr_cmp2(). Q is of order m if LEFT = true
and of order n if LEFT = false.
Synopsis:
call apply_q_qr( mat(:m,:n) , beta(:p) , c(:m) , trans ) call apply_q_qr( mat(:m,:n) , beta(:p) , c(:mc,:nc) , left , trans )
Exemples:

![T =
\left[
\begin{matrix}
T11 & 0 \\
0 & 0
\end{matrix}
\right]](../_images/math/b28c5d6968ecfbe7d45c68b3300ddbc0a2d0a6be.png)
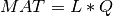
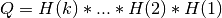
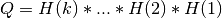
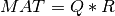
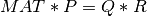
![R = \left[ \begin{matrix} R11 & R12 \\ 0 & R22 \end{matrix} \right] \simeq \left[ \begin{matrix} R11 & R12 \\ 0 & 0 \end{matrix} \right]](../_images/math/4ff8969eef4efe909404b1c832ad2f50a1f07156.png)
![MAT * P \simeq Q * \left[ \begin{matrix} T11 & 0 \\ 0 & 0 \end{matrix} \right] * Z](../_images/math/fd164e159953d8face4b81a106a7c56e5ad5c2de.png)
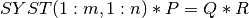
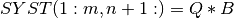
![SYST(1:m,1:n) * P \simeq Q * \left[ \begin{matrix} T11 & 0 \\ 0 & 0 \end{matrix} \right] * Z](../_images/math/54c1213187a03769757fb1835105657433561709.png)