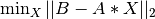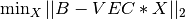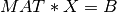MODULE LLSQ_Procedures¶

Module LLSQ_Procedures exports routines for solving linear least squares problems and related computations [Golub_VanLoan:1996] [Lawson_Hanson:1974] [Hansen_etal:2012].

More precisely, routines provided in the LLSQ_Procedures module compute solution of the problem

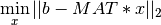
$\min_x || b - MAT * x ||_2$

where MAT is a m-by-n real matrix, b is a m-element vector and x a n-element vector and 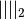$|| ||_2$ is the 2-norm, or of the problem

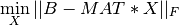
$\min_X || B - MAT * X ||_F$

where MAT, B and X are m-by-n, m-by-p and n-by-p real matrices, respectively, and $|| ||_F$ is the Frobenius norm.

These linear least squares solvers are based on the QR decomposition, the QR decomposition with column pivoting, the Complete Orthogonal Decomposition and the Singular Value Decomposition provided by the QR_Procedures and SVD_Procedures modules.

Assuming for simplicity that m >= n and MAT has full column rank, the QR decomposition of MAT is

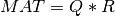
$MAT = Q * R$

and the solution of the (first) linear least square problem is

$x = R^{-1} * [Q^T * b](:n)$

Assuming now that m >= n, but MAT has deficient column rank with 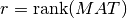$r = {\rm rank}(MAT)$ , the QR decomposition with column pivoting of MAT is

$MAT*P \simeq Q * \left[ \begin{matrix} R11 & R12 \\ 0 & 0 \end{matrix} \right]$

where P is a permutation of the columns of I_n, the identity matrix of order n, R11 is a r-by-r full rank upper triangular matrix and R12 is a r-by-n-r matrix. Using this decomposition, the so-called basic solution of the (first) linear least square problem is now

$x = P * \left( \begin{matrix} R11^{-1} * [Q^T * b](:r) \\ 0 \end{matrix} \right)$

This solution has at least n-r zero components, which corresponds to using only the first r columns of MAT*P in the solution. Interestingly, this implies that the vector b can be approximated by the smallest subset of r columns of MAT. Note, however, that in this case the solution of the linear least square problem is not unique [Lawson_Hanson:1974] [Golub_VanLoan:1996] [Hansen_etal:2012] and it can be demonstrated that the general solution is given by

$x^* = P * \left( \begin{matrix} R11^{-1} * ( [Q^T * b](:r) - R12 * y) \\ y \end{matrix} \right)$

where y is an arbitrary n-r-element vector [Hansen_etal:2012].

Assuming now that MAT is a deficient matrix with 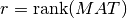$r = {\rm rank}(MAT)$ , the Complete Orthogonal Decomposition (COD) of MAT allows us to compute the unique minimum 2-norm solution of our linear least square problem with

$x = P * Z^T \left( \begin{matrix} T11^{-1} * [Q^T * b](:r) \\ 0 \end{matrix} \right)$

with the COD defined as

$MAT * P = Q * \left[ \begin{matrix} T11 & 0 \\ 0 & 0 \end{matrix} \right] * Z$

where T11 is a r-by-r upper triangular full rank matrix and Z is a n-by-n orthogonal matrix. See description of the QR_Procedures module for more details.

Finally, the Singular Value Decomposition of MAT (which is a special case of the COD described above) allows to compute the generalized inverse of MAT, 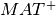$MAT^+$ , by setting to zero the smallest singular values of MAT, which are below a suitable threshold [Lawson_Hanson:1974] [Golub_VanLoan:1996] [Hansen_etal:2012]. Using such generalized inverse, the minimum 2-norm solution of our linear least square problem is given by

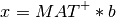
$x = MAT^+ * b$

See the llsq_svd_solve() subroutine for more details.

Please note that routines provided in this module apply only to real data of kind stnd. The real kind type stnd is defined in module Select_Parameters.

In order to use one of these routines, you must include an appropriate use LLSQ_Procedures or use Statpack statement in your Fortran program, like:

use LLSQ_Procedures, only: solve_llsq

or :

use Statpack, only: solve_llsq

Here is the list of the public routines exported by module LLSQ_Procedures:

solve_llsq()¶

Purpose:

solve_llsq() computes a solution to a real linear least squares problem:

$\min_X || B - A * X ||_2$

using an orthogonal factorization with columns pivoting or a Complete Orthogonal Decomposition of A. A is a m-by-n matrix which may be rank-deficient. m>=n or n>m is permitted.

B is a hand side vector or matrix, and X is a solution vector or matrix.

The function returns the solution vector or matrix X. In case of a rank deficient matrix A, the minimum 2-norm solution can be computed at the user option.

Input arguments A and B are not overwritten by solve_llsq().

Synopsis:

x(:n)     = solve_llsq( a(:m,:n) , b(:m)     , krank=krank , tol=tol , min_norm=min_norm )
x(:n,:nb) = solve_llsq( a(:m,:n) , b(:m,:nb) , krank=krank , tol=tol , min_norm=min_norm )
x         = solve_llsq( a(:m)    , b(:m)     )
x(:nb)    = solve_llsq( a(:m)    , b(:m,:nb) )

Synopsis:

ex1_solve_llsq.F90

ex2_solve_llsq.F90

llsq_qr_solve()¶

Purpose:

llsq_qr_solve() computes a solution to a real linear least squares problem:

$\min_X || B - MAT * X ||_2$ or $\min_X || B - VEC * X ||_2$

using an orthogonal factorization with columns pivoting or a Complete Orthogonal Decomposition of MAT. Here MAT is a m-by-n matrix, which may be rank-deficient, m>=n or n>m is permitted, and VEC is a m-vector.

B is a right hand side vector or matrix, and X is a solution vector or matrix.

The subroutine computes the solution vector or matrix X and, optionally, the rank of MAT, the residual vector of the linear least squares problem or its 2-norm. In case of a rank deficient matrix MAT, the minimum 2-norm solution can be computed at the user option.

Input arguments MAT, VEC and B are not overwritten by llsq_qr_solve().

Synopsis:

call llsq_qr_solve( mat(:m,:n) , b(:m)     , x(:n)     , rnorm=rnorm      , resid=resid(:m)     , krank=krank , tol=tol , min_norm=min_norm )
call llsq_qr_solve( mat(:m,:n) , b(:m,:nb) , x(:n,:nb) , rnorm=rnorm(:nb) , resid=resid(:m,:nb) , krank=krank , tol=tol , min_norm=min_norm )
call llsq_qr_solve( vec(:m)    , b(:m)     , x         , rnorm=rnorm      , resid=resid(:m)     )
call llsq_qr_solve( vec(:m)    , b(:m,:nb) , x(:nb)    , rnorm=rnorm(:nb) , resid=resid(:m,:nb) )

Exemples:

ex1_llsq_qr_solve.F90

ex2_llsq_qr_solve.F90

ex3_llsq_qr_solve.F90

llsq_qr_solve2()¶

Purpose:

llsq_qr_solve2() computes a solution to a real linear least squares problem:

$\min_X || B - MAT * X ||_2$ or $\min_X || B - VEC * X ||_2$

using an orthogonal factorization with columns pivoting or a Complete Orthogonal Decomposition of MAT. Here MAT is a m-by-n matrix, which may be rank-deficient, m>=n or n>m is permitted, and VEC is a m-vector.

B is a right hand side vector or matrix, and X is a solution vector or matrix.

The subroutine computes the solution vector or matrix X and, optionally, the rank of MAT, the residual vector of the linear least squares problem or its 2-norm. In case of a rank deficient matrix MAT, the minimum 2-norm solution can be computed at the user option.

Arguments MAT, VEC and B are overwritten with information generated by llsq_qr_solve2().

The orthogonal factorization with columns pivoting or the Complete Orthogonal Decomposition of MAT can be saved in arguments MAT, DIAGR, BETA, IP and TAU on output.

Synopsis:

call llsq_qr_solve2( mat(:m,:n) , b(:m)     , x(:n)     , rnorm=rnorm      , comp_resid=comp_resid , krank=krank , tol=tol , min_norm=min_norm , diagr=diagr(:min(m,n)) , beta=beta(:min(m,n)) , ip=ip(:n) , tau=tau(:min(m,n)) )
call llsq_qr_solve2( mat(:m,:n) , b(:m,:nb) , x(:n,:nb) , rnorm=rnorm(:nb) , comp_resid=comp_resid , krank=krank , tol=tol , min_norm=min_norm , diagr=diagr(:min(m,n)) , beta=beta(:min(m,n)) , ip=ip(:n) , tau=tau(:min(m,n)) )
call llsq_qr_solve2( vec(:m)    , b(:m)     , x         , rnorm=rnorm      , comp_resid=comp_resid , diagr=diagr , beta=beta )
call llsq_qr_solve2( vec(:m)    , b(:m,:nb) , x(:nb)    , rnorm=rnorm(:nb) , comp_resid=comp_resid , diagr=diagr , beta=beta )

Exemples:

ex1_llsq_qr_solve2.F90

ex2_llsq_qr_solve2.F90

qr_solve()¶

Purpose:

qr_solve() solves overdetermined or underdetermined real linear systems

$MAT * X = B$

with a m-by-n matrix MAT, using a QR factorization of MAT as computed by qr_cmp().: m>=n or n>m is permitted, but it is assumed that MAT has full rank.

B is a right hand side vector or matrix, and X is a solution vector or matrix.

It is assumed that qr_cmp() has been used to compute the QR factorization of MAT before qr_solve(). The arguments MAT, DIAGR and BETA give the QR factorization of MAT and assume the same formats as used for the corresponding output arguments of qr_cmp().

Synopsis:

call qr_solve( mat(:m,:n) , diagr(:min(m,n)) , beta(:min(m,n)) , b(:m)     , x(:n)     , rnorm=rnorm      , comp_resid=comp_resid )
call qr_solve( mat(:m,:n) , diagr(:min(m,n)) , beta(:min(m,n)) , b(:m,:nb) , x(:n,:nb) , rnorm=rnorm(:nb) , comp_resid=comp_resid )

Exemples:

ex2_qr_cmp.F90

qr_solve2()¶

Purpose:

qr_solve2() solves overdetermined or underdetermined real linear systems

$MAT * X = B$

with a m-by-n matrix MAT, using an orthogonal factorization with columns pivoting or a Complete Orthogonal Decomposition of MAT as computed by qr_cmp2(). m>=n or n>m is permitted and MAT may be rank-deficient.

B is a right hand side vector or matrix, and X is a solution vector or matrix.

In case of a rank deficient matrix MAT and a Complete Orthogonal Decomposition of MAT is used in input, the minimum 2-norm solution is computed.

It is assumed that qr_cmp2() has been used to compute the orthogonal factorization with columns pivoting or the Complete Orthogonal Decomposition of MAT before qr_solve2(). The arguments MAT, DIAGR, BETA, IP and TAU give the QR factorizations of MAT and assume the same formats as used for the corresponding output arguments of qr_cmp2().

Synopsis:

call qr_solve2( mat(:m,:n) , diagr(:min(m,n)) , beta(:min(m,n)) , ip(:n) , krank , b(:m)     , x(:n)     , rnorm=rnorm      , comp_resid=comp_resid , tau=tau(:min(m,n)) )
call qr_solve2( mat(:m,:n) , diagr(:min(m,n)) , beta(:min(m,n)) , ip(:n) , krank , b(:m,:nb) , x(:n,:nb) , rnorm=rnorm(:nb) , comp_resid=comp_resid , tau=tau(:min(m,n)) )

Exemples:

ex2_qr_cmp2.F90

ex3_qr_cmp2.F90

llsq_svd_solve()¶

Purpose:

llsq_svd_solve() computes the minimum 2-norm solution to a real linear least squares problem:

$\min_X || B - MAT * X ||_2$

using the Singular Value Decomposition (SVD) of MAT. MAT is an m-by-n matrix which may be rank-deficient.

Several right hand side vectors b and solution vectors x can be handled in a single call; they are stored as the columns of the m-by-nrhs right hand side matrix B and the n-by-nrhs solution matrix X, respectively.

The practical rank of MAT, krank, is determined by treating as zero those singular values which are less than TOL times the largest singular value.

Synopsis:

call llsq_svd_solve( mat(:m,:n) , b(:m)     , failure , x(:n)     , singvalues=singvalues(:min(m,n)) , krank=krank , rnorm=rnorm      , tol=tol ,  mul_size=mul_size , maxiter=maxiter , max_francis_steps=max_francis_steps , perfect_shift=perfect_shift )
call llsq_svd_solve( mat(:m,:n) , b(:m,:nb) , failure , x(:n,:nb) , singvalues=singvalues(:min(m,n)) , krank=krank , rnorm=rnorm(:nb) , tol=tol ,  mul_size=mul_size , maxiter=maxiter , max_francis_steps=max_francis_steps , perfect_shift=perfect_shift )

Exemples:

ex1_llsq_svd_solve.F90

ex2_llsq_svd_solve.F90

Previous topic

Next topic

MODULE LLSQ_Procedures¶