MODULE Hous_Procedures¶
Module Hous_Procedures exports subroutines for computing and applying elementary Householder reflectors [Golub_VanLoan:1996] [Lawson_Hanson:1974].
A Householder transformation is a rank-1 modification of the identity matrix which can be used to zero out selected
elements of a vector. A n-by-n Householder reflector matrix H in STATPACK is represented
in the form
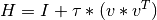
where v is a n-vector, called the Householder vector, and 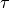 is a scalar.
Note that an Householder reflector matrix
is a scalar.
Note that an Householder reflector matrix H always verify
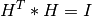
and
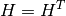
The routines in the Hous_Procedures take into account the rank-1 structure and the orthogonal and symmetry properties of Householder reflectors to create and apply Householder transformations efficiently.
Two different implementations of Householder reflectors are provided here, the first is described in [Anderson_Fahey:1997] and the second in [Lawson_Hanson:1974].
Please note, finally, that routines provided in this module apply only to real data of kind stnd. The real kind type stnd is defined in module Select_Parameters.
In order to use one of these routines, you must include an appropriate use Hous_Procedures or
use Statpack statement in your Fortran program, like:
use Hous_Procedures, only: hous1
or :
use Statpack, only: hous1
Here is the list of the public routines exported by module Hous_Procedures:
-
hous1()¶
purpose:
Given a n-element real vector x (provided in the argument U), hous1() generates a real elementary
reflector H of order n, such that
where beta is a real scalar. H is represented in the form
where tau is a real scalar and v is a n-element real vector with v(1) = 1.
If the elements of x(2:n) are all zero or size(U)=1, then tau = 0
and H is taken to be the unit matrix.
Otherwise 1 <= tau <= 2.
This subroutine is based on the routine DLARFG in LAPACK with improvements suggested by [Anderson_Fahey:1997].
Synopsis:
call hous1( u(:n) , tau ) call hous1( u(:n) , tau , beta )
-
apply_hous1()¶
purpose:
apply_hous1() applies a real elementary reflector H generated by hous1()
to a real vector/matrix C. H is represented in the form
where tau is a real scalar and v is a n-element real vector with v(1) = 1.
If tau = 0, then H is taken to be the unit matrix and C is not modified.
Synopsis:
call apply_hous1( u(:n) , tau , vec(:) ) call apply_hous1( u(:n) , tau , mat(:,:) , left )
-
hous2()¶
purpose:
Given a n-1-element real vector x and a real scalar alpha (provided in the arguments U and PIVOT on entry),
hous2() generates a real elementary reflector H of order n, such that
where beta is a real scalar. H is represented in the form
where tau is a real scalar and v is a n-element real vector with v(1) = 1.
If the elements of x are all zero, then tau = 0 and H is taken to be
the unit matrix.
Otherwise 1 <= tau <= 2.
This subroutine is based on the routine DLARFG in LAPACK with improvements suggested by [Anderson_Fahey:1997].
Synopsis:
call hous2( pivot, u(:n-1) , tau )
-
apply_hous2()¶
purpose:
apply_hous2() applies a real elementary reflector H of order n, generated
by hous2(), to a real vector/matrix C. H is represented in the form
where tau is a real scalar and v is a n-element real vector with v(1) = 1.
More precisely, v is defined as
for the input vector argument U.
Here, the n-element real vector C has the form:
or the real matrix C has the form, if LEFT=true:
or, if LEFT=false:
for given input arguments PIV, VEC or VEC_PIV, MAT.
If tau = 0, then H is taken to be the unit matrix and C is not modified.
Synopsis:
call apply_hous2( u(:n-1) , tau , piv , vec(:) ) call apply_hous2( u(:n-1) , tau , vec_piv(:) , mat(:,:) , left )
-
h1()¶
purpose:
Given a n-element real vector x (provided in the argument U), h1() generates a real elementary
reflector H of order n, such that
where beta is a real scalar. H is represented in the form
where tau is a real scalar and v is a n-element real vector. Note that here, v(1) is not
equal to 1, contrary to the formulation used in hous1().
The real elementary reflector H is then, optionally, applied to a real vector/matrix C.
This subroutine is based on the routine H1 described in [Lawson_Hanson:1974].
Synopsis:
call h1( u(:n) , beta , tau ) call h1( u(:n) , beta , tau , vec(:) ) call h1( u(:n) , beta , tau , mat(:,:) , left )
-
apply_h1()¶
purpose:
apply_h1() applies a real elementary reflector H generated by h1()
to a n-element real vector or to a n-by-m or m-by-n real matrix
from the left or the right. H is represented in the form
where tau is a real scalar and v is a n-element real vector.
Synopsis:
call apply_h1( u(:n) , tau , vec(:) ) call apply_h1( u(:n) , tau , mat(:,:) , left )
-
h2()¶
purpose:
Given a n-1-element real vector x and a real scalar alpha (provided in the arguments U and BETA on entry),
h2() generates a real elementary reflector H of order n, such that
where beta is a real scalar. H is represented in the form
where tau is a real scalar and v is a n-element real vector. Note that here v(1) is not
equal to 1, contrary to the formulation in hous2().
The real elementary reflector H is then, optionally, applied to a real vector/matrix C.
This subroutine is based on the routine H2 described in [Lawson_Hanson:1974].
Synopsis:
call h2( beta, u(:n-1) , up , tau ) call h2( beta, u(:n-1) , up , tau , piv , vec(:) ) call h2( beta, u(:n-1) , up , tau , vec_piv(:) , mat(:) , left )
-
apply_h2()¶
purpose:
apply_h2() applies a real elementary reflector H generated by h2()
to a n-element real vector or to a n-by-m or m-by-n real
matrix from the left or the right. H is represented in the form
where tau is a real scalar and v is a n-element real vector.
More precisely, v is defined as
from the input arguments UP and U.
Here, the n-element real vector C has the form:
or the real matrix C has the form, if LEFT=true:
or, if LEFT=false:
for given input arguments PIV, VEC or VEC_PIV, MAT.
If tau = 0, then H is taken to be the unit matrix and C is not modified.
Synopsis:
call apply_h2( u(:n-1) , up , tau , piv , vec(:) ) call apply_h2( u(:n-1) , up , tau , vec_piv(:) , mat(:,:) , left )

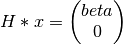
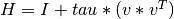
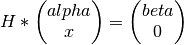
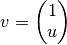
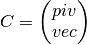
![C = \left[ \begin{matrix} vec\_piv^T \\ MAT \end{matrix} \right]](../_images/math/66b75dfbe783a2dd3235e24d790333553e50fefd.png)
![C = \left[ \begin{matrix} vec\_piv & MAT \end{matrix} \right]](../_images/math/27799536d3f393528278c94095deaf85686ca00c.png)