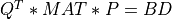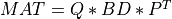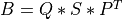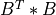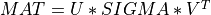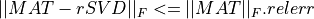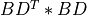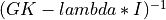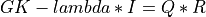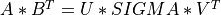MODULE SVD_Procedures¶
Module SVD_Procedures exports a large set of routines for computing the full or partial Singular Value Decomposition (SVD), generalized inverse of a matrix and related computations (e.g. bidiagonal reduction of a general matrix, bidiagonal SVD solvers, …) [Lawson_Hanson:1974] [Golub_VanLoan:1996] . Fast methods for obtaining approximations of a truncated SVD of rectangular matrices or EigenValue Decomposition (EVD) of symmetric positive semi-definite matrices based on randomization algorithms are also included [Halko_etal:2011] [Martinsson:2019].
A general rectangular m-by-n matrix MAT has a SVD into the product of a m-by-min(m,n) orthogonal
matrix U (e.g. 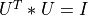 ), a
), a min(m,n)-by-min(m,n) diagonal matrix of singular values SIGMA
and the transpose of a n-by-min(m,n) orthogonal matrix V (e.g. 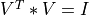 ),
),
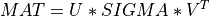
The singular values 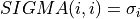 are all non-negative and can be chosen to form a nonincreasing sequence,
are all non-negative and can be chosen to form a nonincreasing sequence,
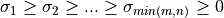
Note that the driver routines in the SVD_Procedures module compute the thin version of the SVD with U and V
as a m-by-min(m,n) and n-by-min(m,n) orthogonal matrices, respectively. This reduces the needed workspace or allows
in-place computation and is the most commonly-used SVD form in practice.
Mathematically, the full SVD is defined with U as a m-by-m orthogonal matrix,
V a a n-by-n orthogonal matrix and SIGMA as a m-by-n diagonal matrix (with additional rows or columns of zeros).
This full SVD can be computed with the help of the computational routines included in the SVD_Procedures module at the user option.
The SVD of a matrix has many practical uses [Lawson_Hanson:1974] [Golub_VanLoan:1996] [Hansen_etal:2012]. The condition
number of the matrix is given by the ratio of the largest singular value to the smallest singular value.
The presence of a zero singular value indicates that the matrix is singular.
The number of non-zero singular values indicates the rank of the matrix. In practice, the SVD of a rank-deficient matrix
will not produce exact zeroes for singular values, due to finite numerical precision. Small singular values should be set to zero explicitly
by choosing a suitable tolerance and this is the strategy followed for computing the generalized (e.g. Moore-Penrose) inverse
MAT+ of a matrix [Golub_VanLoan:1996] [Hansen_etal:2012]. See the documentation of the comp_ginv() subroutine for more details.
For a rank-deficient matrix, the null space of MAT is given by the columns of V corresponding
to the zero singular values in the full SVD of MAT. Similarly, the range of MAT is given by columns of U
corresponding to the non-zero singular values.
See [Lawson_Hanson:1974], [Golub_VanLoan:1996] or [Hansen_etal:2012] for more details on these results.
As intermediate steps for computing the SVD or for obtaining a partial SVD at reduced cost, this module also provides routines for
the transformation of
MATto bidiagonal formBDby similarity transformations [Lawson_Hanson:1974] [Golub_VanLoan:1996],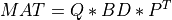
where
QandPare orthogonal matrices andBDis amin(m,n)-by-min(m,n)upper or lower bidiagonal matrix (e.g. with non-zero entries only on the diagonal and superdiagonal or on the diagonal and subdiagonal). The shape ofQism-by-min(m,n)and the shape ofPisn-by-min(m,n).the computation of the singular values
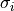 , left singular vectors
, left singular vectors 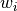 and right singular vectors
and right singular vectors 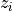 of
of BD,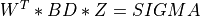
where
SIGMAis amin(m,n)-by-min(m,n)diagonal matrix with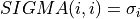 ,
, Wis themin(m,n)-by-min(m,n)matrix of left singular vectors ofBDandZis themin(m,n)-by-min(m,n)matrix of right singular vectors ofBD;the back-transformation of the singular vectors
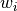 and
and 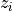 of
of BDto the singular vectors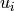 and
and 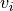 of
of MAT,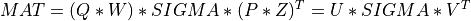
where
Uis them-by-min(m,n)matrix of the left singular vectors ofMAT,Vis then-by-min(m,n)matrix of the right singular vectors ofMATand the singular values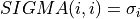 of
of BDare also the singular values ofMAT.
Depending on the situation and the algorithm used, it is also possible to compute only the largest singular values and
associated singular vectors of BD.
STATPACK includes two different algorithms for the transformation of matrix to bidiagonal form:
- a cache-efficient blocked and parallel version of the classic Golub and Kahan Householder bidiagonalization, which reduces the traffic on the data bus from four reads and two writes per column-row elimination of the bidiagonalization process to one read and one write [Howell_etal:2008];
- a blocked and parallel version of the one-sided Ralha-Barlow bidiagonal reduction algorithm [Ralha:2003] [Barlow_etal:2005] [Bosner_Barlow:2007] ,
with partial reorthogonalization based on Gram-Schmidt orthogonalization [Stewart:2007]. This algorithm is significantly faster in most cases, but is slightly
less accurate for the left singular vectors (if
m>=n).
Blocked and parallel routines are also provided for generation and application of the orthogonal matrices, Q and P, associated with the
bidiagonalization process, in both cases [Dongarra_etal:1989] [Golub_VanLoan:1996] [Walker:1988].
Currently, STATPACK includes three different algorithms for computing (selected) singular values and vectors of a bidiagonal matrix BD:
- implicit QR bidiagonal iteration [Lawson_Hanson:1974] [Golub_VanLoan:1996],
- bisection-inverse iteration on the Tridiagonal Golub-Kahan (TGK) form of a bidiagonal matrix [Godunov_etal:1993] [Ipsen:1997] [Dhillon:1998] [Marques_Vasconcelos:2017],
- and a novel bisection-deflation perfect shift technique applied directly to the bidiagonal matrix
BDbased on the works of Godunov and coworkers on deflation for tridiagonal matrices [Godunov_etal:1993] [Fernando:1997] and [Malyshev:2000].
The QR bidiagonal algorithm applies a sequence of similarity transformations to the bidiagonal matrix BD until its off-diagonal elements become
negligible and the diagonal elements have converged to the singular values of BD. It consists of a bulge-chasing procedure that implicitly includes
shifts and use plane rotations (e.g. Givens rotations) which preserve the bidiagonal form of BD [Lawson_Hanson:1974] [Golub_VanLoan:1996].
High performance is obtained in STATPACK by restructuring the QR bidiagonal iteration with a wave-front algorithm for the accumulation of Givens rotations
[VanZee_etal:2011], by the use of a novel perfect shift strategy in the QR iterations inspired by the works of [Godunov_etal:1993] [Malyshev:2000] and [Fernando:1997] and, finally, OpenMP parallelization [Demmel_etal:1993]. Subset computations are not possible with the QR bidiagonal algorithm, with this method it
is possible to compute all the singular values or both all the singular values and associated singular vectors.
Bisection is based on Sturm sequences and requires 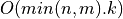 or
or 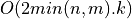 operations to compute
operations to compute k singular values of a
min(n,m)-by-min(n,m) bidiagonal matrix BD [Golub_VanLoan:1996].
Two parallel bisection algorithms for bidiagonal matrices are currently provided in STATPACK:
- The first applies bisection to an associated
2.min(n,m)-by-2.min(n,m)symmetric tridiagonal matrixT(the so-called Tridiagonal Golub-Kahan form ofBD) whose eigenvalues are the singular values ofBDand their negatives [Fernando:1998]; - The second applies bisection implicitly to the associated
min(n,m)-by-min(n,m)symmetric tridiagonal matrixBDT *BDwhose eigenvalues are the squares of the singular values ofBDby using the differential stationary form of the QD algorithm of Rutishauser (see Sec.3.1 of [Fernando:1998]).
If high relative accuracy for small singular values is required, the first algorithm based on the Tridiagonal Golub-Kahan (TGK) form of the
bidiagonal matrix is the best choice [Fernando:1998]. Both STATPACK bidiagonal bisection routines also allow subset computations of the largest singular
values of BD.
Once singular values have been obtained by bisection or implicit QR bidiagonal iteration, associated singular vectors can be computed efficiently using:
- Fernando’s method and inverse iteration on the TGK form of the bidiagonal matrix
BD[Godunov_etal:1993] [Marques_Vasconcelos:2017] [Bini_etal:2005]. These singular vectors are then orthogonalized by the modified Gram-Schmidt algorithm if the singular values are not well-separated; - a novel technique combining an extension to bidiagonal matrices of Fernando’s approach for computing eigenvectors of tridiagonal matrices with a deflation procedure by Givens rotations originally developed by Godunov and collaborators [Fernando:1997] [Parlett_Dhillon:1997] [Malyshev:2000]. If this deflation technique failed, QR bidiagonal iterations with a perfect shift strategy are used instead as a back-up procedure [Mastronardi_etal:2006]. It is highly recommended to compute the singular values of the bidiagonal matrix to high accuracy for the success of the deflation technique, meaning that this approach is less robust than the inverse iteration technique for computing selected singular vectors of a bidiagonal matrix.
If the distance between the singular values of BD is sufficient relative to the norm of BD, then computing the associated singular
vectors by inverse iteration or deflation is also a 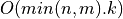 or
or 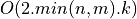 process, where
process, where k is the number of singular
vectors to compute.
Furthermore, subset computations are not possible in the standard implicit QR bidiagonal algorithm, and the bisection-inverse iteration or bisection-deflation
methods are the preferred methods if you are only interested in a subset of the singular vectors of the matrix BD or MAT.
All above algorithms are parallelized with OpenMP [openmp]. Parallelism concerns only the computation of singular vectors in the QR bidiagonal method, but both the computation of the singular values and the singular vectors in the bisection-inverse iteration and bisection-deflation methods.
Note also that the driver and computational routines provided in this module are different from the corresponding implicit QR bidiagonal iteration and inverse iteration routines provided by LAPACK [Anderson_etal:1999] and are much faster if OpenMP and BLAS support are used, but usually less accurate for the same precision in their default settings.
In addition to these standard and accurate driver and computational routines based on implicit QR bidiagonal, inverse or deflation iterations applied to bidiagonal matrices after a preliminary bidagonal reduction step, module SVD_Procedures also includes routines for computing:
- approximations of the largest singular values and associated left and right singular vectors of full matrices using randomized power, subspace or block Krylov iterations [Halko_etal:2011] [Gu:2015] [Musco_Musco:2015] [Li_etal:2017];
- approximations of the largest eigenvalues and associated eigenvectors of full symmetric positive semi-definite matrices using randomized power, subspace or block Krylov iterations and the Nystrom method [Halko_etal:2011] [Musco_Musco:2015] [Li_etal:2017]. The Nystrom method provides more accurate results for positive semi-definite matrices.
For a good introduction to randomized linear algebra, see [Li_etal:2017], [Martinsson:2019] and [Erichson_etal:2019]. There are two classes of randomized low-rank approximation algorithms, sampling-based and random projection-based algorithms:
- Sampling algorithms use randomly selected columns or rows based on sampling probabilities derived from the original matrix in a first step, and a deterministic algorithm, such as SVD or EVD, is performed on the smaller subsampled matrix;
- the projection-based algorithms use the concept of random projections to project the high-dimensional space spanned by the columns of the matrix into a low-dimensional subspace, which approximates the dominant subspace of a matrix. The input matrix is then compressed-either explicitly or implicitly-to this subspace, and the reduced matrix is manipulated inexpensively by standard methods to obtain the desired low-rank factorization in a second step.
The randomized routines included in module SVD_Procedures are projection-based methods. In many cases, this approach beats largely its classical competitors in terms of speed [Halko_etal:2011] [Musco_Musco:2015] [Li_etal:2017]. Thus, these routines based on recent randomized projection algorithms are much faster than the standard drivers included in module SVD_Procedures or Eig_Procedures for computing truncated SVD and EVD of a matrix. Yet, such randomized methods are also shown to compute with a very high probability low-rank approximations that are accurate, and are known to perform even better in many practical situations when the singular values of the input matrix decay quickly [Halko_etal:2011] [Gu:2015] [Li_etal:2017].
The randomized algorithms are also parallelized with OpenMP [openmp].
Finally, note that the routines provided in this module apply only to real data of kind stnd. The real kind type stnd is defined in module Select_Parameters. Computation of singular values and vectors for a complex matrix are not provided in this release of STATPACK.
In order to use one of these routines, you must include an appropriate use SVD_Procedures or use Statpack statement
in your Fortran program, like:
use SVD_Procedures, only: svd_cmp
or :
use Statpack, only: svd_cmp
Here is the list of the public routines exported by module SVD_Procedures:
-
bd_cmp()¶
Purpose:
bd_cmp() reduces a general m-by-n matrix MAT to upper or lower bidiagonal form BD
by an orthogonal transformation:
where Q and P are orthogonal matrices. If:
m>=n,BDis upper bidiagonal;m<n,BDis lower bidiagonal.
bd_cmp() computes BD, Q and P, using an efficient variant of the classic Golub and Kahan Householder
bidiagonalization algorithm [Howell_etal:2008].
Optionally, bd_cmp() can also reduce a general m-by-n matrix MAT to upper bidiagonal form
BD by a two-step algorithm:
If
m>=n, a QR factorization of the realm-by-nmatrixMATis first computed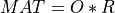
where
Ois orthogonal andRis upper triangular. In a second step, then-by-nupper triangular matrixRis reduced to upper bidiagonal formBDby an orthogonal transformation: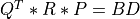
where
QandPare orthogonal andBDis an upper bidiagonal matrix.If
m<n, an LQ factorization of the realm-by-nmatrixMATis first computed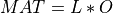
where
Ois orthogonal andLis lower triangular. In a second step, them-by-mlower triangular matrixLis reduced to upper bidiagonal formBDby an orthogonal transformation :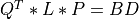
where
QandPare orthogonal andBDis an upper bidiagonal matrix.
This two-step reduction algorithm will be more efficient if m is much larger than n or if n
is much larger than m.
These two different reduction algorithms of MAT to bidiagonal form BD are also parallelized with OpenMP.
Synopsis:
call bd_cmp( mat(:m,:n) , d(:min(m,n)) , e(:min(m,n)) , tauq(:min(m,n)) , taup(:min(m,n)) ) call bd_cmp( mat(:m,:n) , d(:min(m,n)) , e(:min(m,n)) , tauq(:min(m,n)) ) call bd_cmp( mat(:m,:n) , d(:min(m,n)) , e(:min(m,n)) ) call bd_cmp( mat(:m,:n) , d(:min(m,n)) , e(:min(m,n)) , tauq(:min(m,n)) , taup(:min(m,n)), rlmat(:min(m,n),:min(m,n)) , tauo=tauo(:min(m,n)) )
Examples:
-
bd_cmp2()¶
Purpose:
bd_cmp2() reduces a m-by-n matrix MAT with m >= n to upper bidiagonal
form BD by an orthogonal transformation:
where Q and P are orthogonal.
bd_cmp2() computes BD, Q and P using a parallel (if OpenMP support is activated) and blocked version
of the one-sided Ralha-Barlow bidiagonal reduction algorithm [Ralha:2003] [Barlow_etal:2005] [Bosner_Barlow:2007].
bd_cmp2() is more efficient than bd_cmp(), but is less accurate for the computation of the Q orthogonal
matrix.
Synopsis:
call bd_cmp2( mat(:m,:n) , d(:n) , e(:n) , p(:n,:n), failure=failure , gen_p=gen_p ) call bd_cmp2( mat(:m,:n) , d(:n) , e(:n) , failure=failure )
Examples:
-
bd_cmp3()¶
Purpose:
bd_cmp3() reduces a m-by-n matrix MAT with m >= n to upper bidiagonal
form BD by an orthogonal transformation:
where Q and P are orthogonal.
bd_cmp3() computes BD and P using a parallel (if OpenMP support is activated) and blocked version
of the one-sided Ralha-Barlow bidiagonal reduction algorithm [Ralha:2003] [Barlow_etal:2005] [Bosner_Barlow:2007].
bd_cmp3() is faster than bd_cmp2(), if the Q orthogonal matrix is not needed.
Synopsis:
call bd_cmp3( mat(:m,:n) , d(:n) , e(:n) , gen_p=gen_p , failure=failure )
Examples:
-
ortho_gen_bd()¶
Purpose:
ortho_gen_bd() generates the real orthogonal matrices Q and P determined by bd_cmp()
when reducing a m-by-n real matrix MAT to bidiagonal form:
Q and P are defined as products of elementary reflectors H(i) and G(i),
respectively, as computed by bd_cmp() and stored in its array arguments MAT, TAUQ and TAUP.
If m >= n:
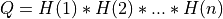 and ortho_gen_bd() returns the first
and ortho_gen_bd() returns the first ncolumns ofQin MAT;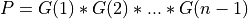 and ortho_gen_bd() returns
and ortho_gen_bd() returns Pas ann-by-nmatrix in P.
If m < n:
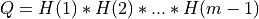 and ortho_gen_bd() returns
and ortho_gen_bd() returns Qas anm-by-mmatrix in MAT(1:m,1:m);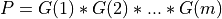 and ortho_gen_bd() returns the first
and ortho_gen_bd() returns the first mcolumns ofP, in P.
The generation of the real orthogonal matrices Q and P is blocked and parallelized with OpenMP [Walker:1988].
Synopsis:
call ortho_gen_bd( mat(:m,:n) , tauq(:min(m,n)) , taup(:min(m,n)) , p(:n,:min(m,n)) )
Examples:
-
ortho_gen_bd2()¶
Purpose:
ortho_gen_bd2() generates the real orthogonal matrices Q and PT determined by bd_cmp()
when reducing a m-by-n real matrix MAT to bidiagonal form:
Q and PT are defined as products of elementary reflectors H(i) and G(i),
respectively, as computed by bd_cmp() and stored in its array arguments MAT, TAUQ and TAUP.
If m >= n:
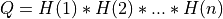 and ortho_gen_bd2() returns the first
and ortho_gen_bd2() returns the first ncolumns ofQin MAT;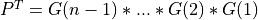 and ortho_gen_bd2() returns
and ortho_gen_bd2() returns PT as ann-by-nmatrix in Q_PT.
If m < n:
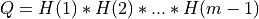 and ortho_gen_bd2() returns
and ortho_gen_bd2() returns Qas anm-by-mmatrix in Q_PT; and ortho_gen_bd2() returns the first
and ortho_gen_bd2() returns the first mrows ofPT, in MAT.
The generation of the real orthogonal matrices Q and PT is blocked and parallelized with OpenMP [Walker:1988].
Synopsis:
call ortho_gen_bd2( mat(:m,:n) , tauq(:min(m,n)) , taup(:min(m,n)) , q_pt(:min(m,n),:min(m,n)) )
-
ortho_gen_q_bd()¶
Purpose:
ortho_gen_q_bd() generate the real orthogonal matrix Q determined by bd_cmp()
when reducing a m-by-n real matrix MAT to bidiagonal form:
Q is defined as products of elementary reflectors H(i) as computed by bd_cmp()
and stored in its array arguments MAT and TAUQ.
If m >= n:
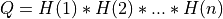 and ortho_gen_q_bd() returns the first
and ortho_gen_q_bd() returns the first ncolumns ofQin MAT;
If m < n:
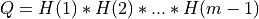 and ortho_gen_q_bd() returns
and ortho_gen_q_bd() returns Qas anm-by-mmatrix in MAT(1:m,1:m);
The generation of the real orthogonal matrix Q is blocked and parallelized with OpenMP [Walker:1988].
Synopsis:
call ortho_gen_q_bd( mat(:m,:n) , tauq(:min(m,n)) )
Examples:
-
ortho_gen_p_bd()¶
Purpose:
ortho_gen_p_bd() generate the real orthogonal matrix P determined by bd_cmp()
when reducing a m-by-n real matrix MAT to bidiagonal form:
P is defined as products of elementary reflectors G(i) determined by bd_cmp()
and stored in its array arguments MAT and TAUP.
If m >= n:
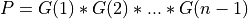 and ortho_gen_p_bd() returns
and ortho_gen_p_bd() returns Pas ann-by-nmatrix in P.
If m < n:
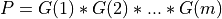 and ortho_gen_p_bd() returns the first
and ortho_gen_p_bd() returns the first mcolumns ofP, in P.
The generation of the real orthogonal matrix P is blocked and parallelized with OpenMP [Walker:1988].
Synopsis:
call ortho_gen_p_bd( mat(:m,:n) , taup(:min(m,n)) , p(:n,:min(m,n)) )
Examples:
-
apply_q_bd()¶
Purpose:
apply_q_bd() overwrites the general real m-by-n matrix C with:
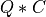 if LEFT =
if LEFT = trueand TRANS =false;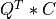 if LEFT =
if LEFT = trueand TRANS =true;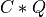 if LEFT =
if LEFT = falseand TRANS =false;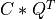 if LEFT =
if LEFT = falseand TRANS =true.
Here Q is the orthogonal matrix determined by bd_cmp() when reducing
a real matrix MAT to bidiagonal form:
and Q is defined as products of elementary reflectors H(i).
Let nq = m if LEFT = true and nq = n if LEFT = false. Thus, nq is the
order of the orthogonal matrix Q that is applied. MAT is assumed to
have been an nq-by-k matrix and
, if
nq >= k;
or
, if
nq < k.
The application of the real orthogonal matrix Q to the matrix C is blocked and parallelized with OpenMP [Walker:1988].
Synopsis:
call apply_q_bd( mat(:m,:n) , tauq(:min(m,n)) , c(:,:) , left , trans )
Examples:
-
apply_p_bd()¶
Purpose:
apply_p_bd() overwrites the general real m-by-n matrix C with
if LEFT =
trueand TRANS =false;if LEFT =
trueand TRANS =true;if LEFT =
falseand TRANS =false;if LEFT =
falseand TRANS =true.
Here P is the orthogonal matrix determined by bd_cmp() when reducing
a real matrix MAT to bidiagonal form:
and P is defined as products of elementary reflectors G(i).
Let np = m if LEFT = true and np = n if LEFT = false. Thus, np is the
order of the orthogonal matrix P that is applied. MAT is assumed to
have been an k-by-np matrix and
, if
k < np;
or
, if
k >= np.
The application of the real orthogonal matrix P to the matrix C is blocked and parallelized with OpenMP [Walker:1988].
Synopsis:
call apply_p_bd( mat(:m,:n) , taup(:min(m,n)) , c(:,:) , left , trans )
Examples:
-
bd_svd()¶
Purpose:
bd_svd() computes the singular value decomposition (SVD) of a real
n-by-n (upper or lower) bidiagonal matrix B:
where S is a diagonal matrix with non-negative diagonal
elements (the singular values of B), and, Q and P are
orthogonal matrices (PT denotes the transpose of P).
The routine computes S, U * Q, and V * P, for given real input
matrices U, V.
Synopsis:
call bd_svd( upper , d(:n) , e(:n) , failure , u(:,:n) , v(:,:n) , sort=sort , maxiter=maxiter , max_francis_steps=max_francis_steps , perfect_shift=perfect_shift ) call bd_svd( upper , d(:n) , e(:n) , failure , u(:,:n) , sort=sort , maxiter=maxiter , max_francis_steps=max_francis_steps , perfect_shift=perfect_shift ) call bd_svd( upper , d(:n) , e(:n) , failure , sort=sort , maxiter=maxiter )
Exemples:
-
bd_svd2()¶
Purpose:
bd_svd2() computes the singular value decomposition (SVD) of a real
n-by-n (upper or lower) bidiagonal matrix B:
where S is a diagonal matrix with non-negative diagonal
elements (the singular values of B), and, Q and P are
orthogonal matrices (PT denotes the transpose of P).
The routine computes S, U * Q, and PT * VT,
for given real input matrices U, VT.
Synopsis:
call bd_svd2( upper , d(:n) , e(:n) , failure , u(:,:n) , vt(:n,:) , sort=sort , maxiter=maxiter , max_francis_steps=max_francis_steps , perfect_shift=perfect_shift ) call bd_svd2( upper , d(:n) , e(:n) , failure , u(:,:n) , sort=sort , maxiter=maxiter , max_francis_steps=max_francis_steps , perfect_shift=perfect_shift ) call bd_svd2( upper , d(:n) , e(:n) , failure , sort=sort , maxiter=maxiter )
Exemples:
-
bd_singval()¶
Purpose:
bd_singval() computes all or some of the greatest singular values of a real n-by-n
(upper or lower) bidiagonal matrix B by a bisection algorithm.
The Singular Value Decomposition of B is:
where S is a diagonal matrix with non-negative diagonal elements (the singular
values of B), and, Q and P are orthogonal matrices (PT denotes the transpose of P).
The singular values S of the bidiagonal matrix B are computed by a bisection algorithm applied to
the Tridiagonal Golub-Kahan (TGK) form of the bidiagonal matrix B (see [Fernando:1998]; Sec.3.3 ).
The singular values can be computed with high relative accuracy, at the user option, by using the optional
argument ABSTOL with the value sqrt(lamch("S")).
Synopsis:
call bd_singval( d(:n) , e(:n) , nsing , s(:n) , failure , sort=sort , vector=vector , abstol=abstol , ls=ls , theta=theta , scaling=scaling , init=init )
Examples:
-
bd_singval2()¶
Purpose:
bd_singval2() computes all or some of the greatest singular values of a real n-by-n
(upper or lower) bidiagonal matrix B by a bisection algorithm.
The Singular Value Decomposition of B is:
where S is a diagonal matrix with non-negative diagonal elements (the singular
values of B), and, Q and P are orthogonal matrices (PT denotes the transpose of P).
The singular values S of the bidiagonal matrix B are computed by a bisection algorithm (see [Golub_VanLoan:1996]; Sec.8.5 ).
The bisection method is applied (implicitly) to the associated n-by-n symmetric tridiagonal matrix
whose eigenvalues are the squares of the singular values of B by using the differential stationary
form of the qd algorithm of Rutishauser (see [Fernando:1998]; Sec.3.1 ).
The singular values can be computed with high accuracy at the user option.
The singular values can be computed with high relative accuracy, at the user option, by using the optional
argument ABSTOL with the value sqrt(lamch("S")).
Synopsis:
call bd_singval2( d(:n) , e(:n) , nsing , s(:n) , failure , sort=sort , vector=vector , abstol=abstol , ls=ls , theta=theta , scaling=scaling , init=init )
Examples:
-
svd_cmp()¶
Purpose:
svd_cmp() computes the Singular Value Decomposition (SVD) of a real
m-by-n matrix MAT. The SVD is written:
where SIGMA is an m-by-n matrix which is zero except for its
min(m,n) diagonal elements, U is an m-by-m orthogonal matrix, and
V is an n-by-n orthogonal matrix. The diagonal elements of SIGMA
are the singular values of MAT; they are real and non-negative.
The columns of U and V are, respectively, the left and right singular vectors of MAT.
svd_cmp() computes only the first min(m,n) columns of U and V (e.g. the left
and right singular vectors of MAT in the thin SVD of MAT).
The routine returns the min(m,n) singular values and the associated left and right singular vectors.
Synopsis:
call svd_cmp( mat(:m,:n) , s(:min(m,n)) , failure , v(:n,:min(m,n)) , sort=sort , mul_size=mul_size , maxiter=maxiter , max_francis_steps=max_francis_steps , perfect_shift=perfect_shift , use_svd2=use_svd2 ) call svd_cmp( mat(:m,:n) , s(:min(m,n)) , failure , sort=sort , mul_size=mul_size , maxiter=maxiter , d=d(:min(m,n)) , e=e(:min(m,n)) , tauq=tauq(:min(m,n)) , taup=taup(:min(m,n)) )
Examples:
-
svd_cmp2()¶
Purpose:
svd_cmp2() computes the Singular Value Decomposition (SVD) of a real
m-by-n matrix MAT. The SVD is written:
where SIGMA is an m-by-n matrix which is zero except for its
min(m,n) diagonal elements, U is an m-by-m orthogonal matrix, and
V is an n-by-n orthogonal matrix. The diagonal elements of SIGMA
are the singular values of MAT; they are real and non-negative.
The columns of U and V are, respectively, the left and right singular vectors of MAT.
svd_cmp2() computes only the first min(m,n) columns of U and V (e.g. the left
and right singular vectors of MAT in the thin SVD of MAT). The right singular vectors are
returned rowwise.
This routine uses the same output formats for the SVD factors than the LAPACK SVD routines [Anderson_etal:1999], but
is slower than svd_cmp().
Synopsis:
call svd_cmp2( mat(:m,:n) , s(:min(m,n)) , failure , u_vt(:min(m,n),:min(m,n)) , sort=sort , mul_size=mul_size , maxiter=maxiter , max_francis_steps=max_francis_steps , perfect_shift=perfect_shift , use_svd2=use_svd2 ) call svd_cmp2( mat(:m,:n) , s(:min(m,n)) , failure , sort=sort , mul_size=mul_size , maxiter=maxiter , d=d(:min(m,n)) , e=e(:min(m,n)) , tauq=tauq(:min(m,n)) , taup=taup(:min(m,n)) )
Examples:
-
svd_cmp3()¶
Purpose:
svd_cmp3() computes the Singular Value Decomposition (SVD) of a real
m-by-n matrix MAT. The SVD is written:
where SIGMA is an m-by-n matrix which is zero except for its
min(m,n) diagonal elements, U is an m-by-m orthogonal matrix, and
V is an n-by-n orthogonal matrix. The diagonal elements of SIGMA
are the singular values of MAT; they are real and non-negative.
The columns of U and V are, respectively, the left and right
singular vectors of MAT.
The routine returns the first min(m,n) singular values and the associated
left and right singular vectors corresponding to a thin SVD of MAT.
The right singular vectors are returned rowwise if m<n.
This routine is usually significantly faster than svd_cmp() or svd_cmp2()
because of the use of the Ralha-Barlow one-sided bidiagonalization algorithm in the first step
of the SVD [Barlow_etal:2005] [Bosner_Barlow:2007].
Synopsis:
call svd_cmp3( mat(:m,:n) , s(:min(m,n)) , failure , u_v(:min(m,n),:min(m,n)) , sort=sort , maxiter=maxiter , max_francis_steps=max_francis_steps , perfect_shift=perfect_shift , failure_bd=failure_bd ) call svd_cmp3( mat(:m,:n) , s(:min(m,n)) , failure , sort=sort , maxiter=maxiter , save_mat=save_mat , failure_bd=failure_bd )
Examples:
-
svd_cmp4()¶
Purpose:
svd_cmp4() computes the Singular Value Decomposition (SVD) of a real
m-by-n matrix MAT with m>=n. The SVD is written:
where SIGMA is an m-by-n matrix which is zero except for its
min(m,n) diagonal elements, U is an m-by-m orthogonal matrix, and
V is an n-by-n orthogonal matrix. The diagonal elements of SIGMA
are the singular values of MAT; they are real and non-negative.
The columns of U and V are, respectively, the left and right
singular vectors of MAT.
The routine returns the first data:n singular values and associated left and right singular vectors corresponding
to a thin SVD of MAT.
Optionally, if the logical argument SING_VEC is used with the value false,
the routine computes only the singular values and the orthogonal matrices
Q and P used to reduce MAT to bidiagonal form BD. This is useful
for computing a partial SVD of the matrix MAT with subroutines
bd_inviter2() or bd_deflate2() for example.
This routine is usually significantly faster than svd_cmp() or svd_cmp2()
for computing the thin SVD of MAT because of the use of the Ralha-Barlow one-sided bidiagonalization algorithm
in the first step of the SVD [Barlow_etal:2005] [Bosner_Barlow:2007].
Synopsis:
call svd_cmp4( mat(:m,:n) , s(:n) , failure , v(:n,:n) , sort=sort , maxiter=maxiter , max_francis_steps=max_francis_steps , perfect_shift=perfect_shift , sing_vec=sing_vec , gen_p=gen_p , failure_bd=failure_bd , d(:n), e(:n) ) call svd_cmp4( mat(:m,:n) , s(:n) , failure , sort=sort , maxiter=maxiter , save_mat=save_mat , failure_bd=failure_bd )
Examples:
-
rsvd_cmp()¶
Purpose:
rsvd_cmp() computes approximations of the nsvd largest singular values and associated
left and right singular vectors of a full real m-by-n matrix MAT using
randomized power, subspace or block Krylov iterations [Halko_etal:2011] [Musco_Musco:2015] [Martinsson:2019].
This routine is always significantly faster than svd_cmp(), svd_cmp2(), svd_cmp3(), svd_cmp4()
or bd_inviter2() and bd_deflate2() because of the use of very fast randomized
algorithms [Halko_etal:2011] [Gu:2015] [Musco_Musco:2015] [Martinsson:2019]. However, the computed nsvd
largest singular values and associated left and right singular vectors are only approximations of the
true largest singular values and vectors.
The routine returns approximations to the first nsvd singular values and the associated
left and right singular vectors corresponding to a partial SVD of MAT.
Synopsis:
call rsvd_cmp( mat(:m,:n) , s(:nsvd) , leftvec(:m,:nsvd) , rightvec(:n,:nsvd) , failure=failure , niter=niter , nover=nover , ortho=ortho , extd_samp=extd_samp , rng_alg=rng_alg , maxiter=maxiter , max_francis_steps=max_francis_steps , perfect_shift=perfect_shift )
Examples:
-
rsvd_cmp_fixed_precision()¶
Purpose:
rsvd_cmp_fixed_precision() computes approximations of the top nsvd singular values and associated
left and right singular vectors of a full real m-by-n matrix MAT using
randomized power or subspace iterations [Halko_etal:2011] [Li_etal:2017] [Yu_etal:2018].
nsvd is the target rank of the partial Singular Value Decomposition (SVD), which is sought,
and this partial SVD must have an approximation error which fulfills:
, where rSVD is the computed partial SVD approximation,  is the Frobenius norm and
is the Frobenius norm and
relerr is a prescribed accuracy tolerance for the relative error of the computed partial SVD
approximation in the Frobenius norm, specified as an argument (e.g., argument RELERR) in the call
to rsvd_cmp_fixed_precision().
In other words, nsvd is not known in advance and is determined in the subroutine. This explains
why the output real array arguments S, LEFTVEC and RIGHTVEC, which contain the computed singular
triplets of the partial SVD on exit, must be declared in the calling program as pointers.
On exit, nsvd is equal to the size of the output real pointer argument S, which contains the
computed singular values and the relative error in the Frobenius norm
of the computed partial SVD approximation is output in argument RELERR.
rsvd_cmp_fixed_precision() searches incrementally the best (e.g., smallest) partial SVD approximation, which fulfills the prescribed accuracy tolerance for the relative error based on an improved version of the randQB_FP algorithm described in [Yu_etal:2018]. See also [Martinsson_Voronin:2016]. More precisely, the rank of the partial SVD approximation is increased progressively of BLK_SIZE by BLK_SIZE until the prescribed accuracy tolerance is satisfied and than improved and adjusted precisely by additional subspace iterations (as specified by the optional NITER_QB integer argument) to obtain the smallest partial SVD approximation, which satisfies the prescribed tolerance.
As rsvd_cmp(), this routine is always significantly faster than svd_cmp(), svd_cmp2(), svd_cmp3(), svd_cmp4()
or bd_inviter2() and bd_deflate2() because of the use of very fast randomized
algorithms [Halko_etal:2011] [Gu:2015] [Li_etal:2017] [Yu_etal:2018]. However, the computed nsvd
largest singular values and associated left and right singular vectors are only approximations of the
true largest singular values and vectors.
Note, finally, that if you already know the rank of the partial SVD of MAT you are seeking, it is better
to use rsvd_cmp() rather than rsvd_cmp_fixed_precision() as rsvd_cmp() is faster and slightly more
accurate.
Synopsis:
call rsvd_cmp_fixed_precision( mat(:m,:n) , relerr, s(:) , leftvec(:,:) , rightvec(:,:) , failure_relerr=failure_relerr , failure=failure , niter=niter , blk_size=blk_size , maxiter_qb=maxiter_qb , ortho=ortho , reortho=reortho , niter_qb=niter_qb , rng_alg=rng_alg , maxiter=maxiter , max_francis_steps=max_francis_steps , perfect_shift=perfect_shift )
Examples:
ex1_rsvd_cmp_fixed_precision.F90
-
reig_pos_cmp()¶
Purpose:
reig_pos_cmp() computes approximations of the neig largest eigenvalues and associated
eigenvectors of a full real n-by-n symmetric positive semi-definite matrix MAT using
randomized power, subspace or block Krylov iterations [Halko_etal:2011] [Musco_Musco:2015] [Martinsson:2019] and,
at the user option, the Nystrom method [Li_etal:2017], [Martinsson:2019] [Halko_etal:2011].
The Nystrom method provides more accurate results for positive semi-definite matrices [Halko_etal:2011] [Martinsson:2019].
The Nystrom method will be selected in reig_pos_cmp() if the optional logical
argument USE_NYSTROM is used with the value true (this is the default), otherwise
the standard EVD algorithm will be used in the last step of the randomized algorithm.
This routine is always significantly faster than eig_cmp(), eig_cmp2(), eig_cmp3()
or trid_inviter() and trid_deflate() in module Eig_Procedures because of the use
of very fast randomized algorithms [Halko_etal:2011] [Gu:2015] [Musco_Musco:2015] [Martinsson:2019]. However, the computed neig
largest eigenvalues and eigenvectors are only approximations of the true largest eigenvalues and eigenvectors.
The routine returns approximations to the first neig eigenvalues and the associated
eigenvectors corresponding to a partial EVD of a symmetric positive semi-definite matrix MAT.
Synopsis:
call reig_pos_cmp( mat(:n,:n) , eigval(:neig) , eigvec(:n,:neig) , failure=failure , niter=niter , nover=nover , ortho=ortho , extd_samp=extd_samp , use_nystrom=use_nystrom , rng_alg=rng_alg , maxiter=maxiter , max_francis_steps=max_francis_steps , perfect_shift=perfect_shift )
Examples:
-
singvalues()¶
Purpose:
singvalues() computes the singular values of a real m-by-n matrix MAT.
The Singular Value decomposition (SVD) is written
where SIGMA is an m-by-n matrix which is zero except for its
min(m,n) diagonal elements, U is an m-by-m orthogonal matrix, and
V is an n-by-n orthogonal matrix. The diagonal elements of SIGMA
are the singular values of MAT; they are real and non-negative.
The singular values are computed by the QR bidiagonal algorithm [Lawson_Hanson:1974] [Golub_VanLoan:1996].
Synopsis:
singval(:min(m,n)) = singvalues( mat(:m,:n) , sort=sort , mul_size=mul_size , maxiter=maxiter )
Examples:
-
select_singval_cmp()¶
Purpose:
select_singval_cmp() computes all or some of the greatest singular values of
a real m-by-n matrix MAT.
The Singular Value decomposition (SVD) is written:
where SIGMA is an m-by-n matrix which is zero except for its
min(m,n) diagonal elements, U is an m-by-m orthogonal matrix, and
V is an n-by-n orthogonal matrix. The diagonal elements of SIGMA
are the singular values of MAT; they are real and non-negative.
Both a one-step and a two-step algorithms are available in select_singval_cmp() for the preliminary reduction of the
input matrix MAT to bidiagonal form.
In the one-step algorithm, the original matrix MAT is directly reduced to upper or lower
bidiagonal form BD by an orthogonal transformation:
where Q and P are orthogonal (see [Golub_VanLoan:1996] [Lawson_Hanson:1974] [Howell_etal:2008]).
In the two-step algorithm, the original matrix MAT is also reduced to upper bidiagonal form BD, but if:
m>=n, a QR factorization of the realm-by-nmatrixMATis first computed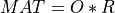
where
Ois orthogonal andRis upper triangular. In a second step, then-by-nupper triangular matrixRis reduced to upper bidiagonal formBDby an orthogonal transformation: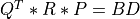
where
QandPare orthogonal andBDis an upper bidiagonal matrix.m<n, an LQ factorization of the realm-by-nmatrixMATis first computed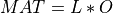
where
Ois orthogonal andLis lower triangular. In a second step, them-by-mlower triangular matrixLis also reduced to upper bidiagonal formBDby an orthogonal transformation :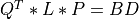
where
QandPare orthogonal andBDis also an upper bidiagonal matrix.
This two-step reduction algorithm will be more efficient if m is much larger than n or if n
is much larger than m.
In both the one-step and two-step algorithms, the singular values SIGMA of the bidiagonal matrix BD, which are
also the singular values of MAT, are then computed by a bisection algorithm applied to the Tridiagonal Golub-Kahan (TGK) form
of the bidiagonal matrix BD (see [Fernando:1998]; Sec.3.3 ).
The routine outputs (parts of) SIGMA and optionally Q and P (in packed form), and
BD for a given matrix MAT. If the two-step algorithm is used, the routine outputs also O explicitly or in a packed form.
SIGMA, Q, P and BD (and also O if the two-step algorithm is selected) may then be used to obtain selected
singular vectors with subroutines bd_inviter2() or bd_deflate2().
Synopsis:
call select_singval_cmp( mat(:m,:n) , nsing , s(:min(m,n)) , failure , sort=sort , mul_size=mul_size , vector=vector , abstol=abstol , ls=ls , theta=theta , d=d(:min(m,n)) , e=e(:min(m,n)) , tauq=tauq(:min(m,n)) , taup=taup(:min(m,n)) , scaling=scaling , init=init ) call select_singval_cmp( mat(:m,:n) , rlmat(:min(m,n),:min(m,n)) , nsing , s(:min(m,n)) , failure , sort=sort , mul_size=mul_size , vector=vector , abstol=abstol , ls=ls , theta=theta , d=d(:min(m,n)) , e=e(:min(m,n)) , tauo=tauo(:min(m,n)) , tauq=tauq(:min(m,n)) , taup=taup(:min(m,n)) , scaling=scaling , init=init )
Examples:
-
select_singval_cmp2()¶
Purpose:
select_singval_cmp2() computes all or some of the greatest singular values of
a real m-by-n matrix MAT.
The Singular Value decomposition (SVD) is written:
where SIGMA is an m-by-n matrix which is zero except for its
min(m,n) diagonal elements, U is an m-by-m orthogonal matrix, and
V is an n-by-n orthogonal matrix. The diagonal elements of SIGMA
are the singular values of MAT; they are real and non-negative.
Both a one-step and a two-step algorithms are available in select_singval_cmp2() for the preliminary reduction of the
input matrix MAT to bidiagonal form.
In the one-step algorithm, the original matrix MAT is directly reduced to upper or lower
bidiagonal form BD by an orthogonal transformation:
where Q and P are orthogonal (see [Golub_VanLoan:1996] [Lawson_Hanson:1974] [Howell_etal:2008]).
In the two-step algorithm, the original matrix MAT is also reduced to upper bidiagonal form BD, but if:
m>=n, a QR factorization of the realm-by-nmatrixMATis first computed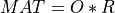
where
Ois orthogonal andRis upper triangular. In a second step, then-by-nupper triangular matrixRis reduced to upper bidiagonal formBDby an orthogonal transformation: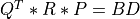
where
QandPare orthogonal andBDis an upper bidiagonal matrix.m<n, an LQ factorization of the realm-by-nmatrixMATis first computed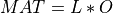
where
Ois orthogonal andLis lower triangular. In a second step, them-by-mlower triangular matrixLis also reduced to upper bidiagonal formBDby an orthogonal transformation :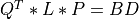
where
QandPare orthogonal andBDis an upper bidiagonal matrix.
This two-step reduction algorithm will be more efficient if m is much larger than n or if n
is much larger than m.
In both the one-step and two-step algorithms, the singular values SIGMA of the bidiagonal matrix BD, which
are also the singular values of MAT, are then computed by a bisection algorithm (see [Golub_VanLoan:1996]; Sec.8.5 ).
The bisection method is applied (implicitly) to the associated min(m,n)-by-min(m,n) symmetric tridiagonal matrix
whose eigenvalues are the squares of the singular values of BD by using the differential stationary
form of the QD algorithm of Rutishauser (see [Fernando:1998]; Sec.3.1 ).
The routine outputs (parts of) SIGMA and optionally Q and P (in packed form), and
BD for a given matrix MAT. If the two-step algorithm is used, the routine outputs also O explicitly or in a packed form.
SIGMA, Q, P and BD (and also O if the two-step algorithm is selected) may then be used to obtain selected
singular vectors with subroutines bd_inviter2() or bd_deflate2().
select_singval_cmp2() is faster than select_singval_cmp(), but is slightly less accurate.
Synopsis:
call select_singval_cmp2( mat(:m,:n) , nsing , s(:min(m,n)) , failure , sort=sort , mul_size=mul_size , vector=vector , abstol=abstol , ls=ls , theta=theta , d=d(:min(m,n)) , e=e(:min(m,n)) , tauq=tauq(:min(m,n)) , taup=taup(:min(m,n)) , scaling=scaling , init=init ) call select_singval_cmp2( mat(:m,:n) , rlmat(:min(m,n),:min(m,n)) , nsing , s(:min(m,n)) , failure , sort=sort , mul_size=mul_size , vector=vector , abstol=abstol , ls=ls , theta=theta , d=d(:min(m,n)) , e=e(:min(m,n)) , tauo=tauo(:min(m,n)) , tauq=tauq(:min(m,n)) , taup=taup(:min(m,n)) , scaling=scaling , init=init )
Examples:
-
select_singval_cmp3()¶
Purpose:
select_singval_cmp3() computes all or some of the greatest singular values of
a real m-by-n matrix MAT with m>=n.
The Singular Value decomposition (SVD) is written:
where SIGMA is an m-by-n matrix which is zero except for its
min(m,n) diagonal elements, U is an m-by-m orthogonal matrix, and
V is an n-by-n orthogonal matrix. The diagonal elements of SIGMA
are the singular values of MAT; they are real and non-negative.
Both a one-step and a two-step algorithms are available in select_singval_cmp3() for the preliminary reduction of the
input matrix MAT to bidiagonal form.
In the one-step algorithm, the original matrix MAT is directly reduced to upper
bidiagonal form BD by an orthogonal transformation:
where Q and P are orthogonal (see [Lawson_Hanson:1974] [Golub_VanLoan:1996]). The fast Ralha-Barlow
one-sided method is used for this purpose (see [Ralha:2003] [Barlow_etal:2005] [Bosner_Barlow:2007]).
In the two-step algorithm, the original matrix MAT is also reduced to upper bidiagonal form BD. But,
a QR factorization of the real m-by-n matrix MAT is first computed
where O is orthogonal and R is upper triangular. In a second step, the n-by-n upper
triangular matrix R is reduced to upper bidiagonal form BD by an orthogonal transformation:
where Q and P are orthogonal and BD is an upper bidiagonal matrix. The fast Ralha-Barlow
one-sided method is also used for this purpose (see [Ralha:2003] [Barlow_etal:2005] [Bosner_Barlow:2007]).
This two-step reduction algorithm will be more efficient if m is much larger than n.
In both the one-step and two-step algorithms, the singular values SIGMA of the bidiagonal matrix BD,
which are also the singular values of MAT, are then computed by a bisection algorithm applied to the Tridiagonal Golub-Kahan form
of the bidiagonal matrix BD (see [Fernando:1998]; Sec.3.3 ).
The routine outputs (parts of) SIGMA, Q and optionally P (in packed form) and
BD for a given matrix MAT. If the two-step algorithm is used, the routine outputs also O explicitly or in a packed form.
SIGMA, Q, P and BD (and also O if the two-step algorithm is selected) may then be used to obtain selected
singular vectors with subroutines bd_inviter2() or bd_deflate2().
select_singval_cmp3() is faster than select_singval_cmp(), but is slightly less accurate.
Synopsis:
call select_singval_cmp3( mat(:m,:n) , nsing , s(:n) , failure , sort=sort , mul_size=mul_size , vector=vector , abstol=abstol , ls=ls , theta=theta , d=d(:n) , e=e(:n) , p=p(:n,:n) , gen_p=gen_p , scaling=scaling , init=init , failure_bd=failure_bd ) call select_singval_cmp3( mat(:m,:n) , rlmat(:min(m,n),:min(m,n)) , nsing , s(:n) , failure , sort=sort , mul_size=mul_size , vector=vector , abstol=abstol , ls=ls , theta=theta , d=d(:n) , e=e(:n) , tauo=tauo(:min(m,n)) , p=p(:n,:n) , gen_p=gen_p , scaling=scaling , init=init , failure_bd=failure_bd )
Examples:
ex1_select_singval_cmp3_bis.F90
ex2_select_singval_cmp3_bis.F90
-
select_singval_cmp4()¶
Purpose:
select_singval_cmp4() computes all or some of the greatest singular values of
a real m-by-n matrix MAT with m>=n.
The Singular Value decomposition (SVD) is written:
where SIGMA is an m-by-n matrix which is zero except for its
min(m,n) diagonal elements, U is an m-by-m orthogonal matrix, and
V is an n-by-n orthogonal matrix. The diagonal elements of SIGMA
are the singular values of MAT; they are real and non-negative.
Both a one-step and a two-step algorithms are available in select_singval_cmp3() for the preliminary reduction of the
input matrix MAT to bidiagonal form.
In the one-step algorithm, the original matrix MAT is directly reduced to upper
bidiagonal form BD by an orthogonal transformation:
where Q and P are orthogonal (see [Lawson_Hanson:1974] [Golub_VanLoan:1996]). The fast Ralha-Barlow
one-sided method is used for this purpose (see [Ralha:2003] [Barlow_etal:2005] [Bosner_Barlow:2007]).
In the two-step algorithm, the original matrix MAT is also reduced to upper bidiagonal form BD. But,
a QR factorization of the real m-by-n matrix MAT is first computed
where O is orthogonal and R is upper triangular. In a second step, the n-by-n upper
triangular matrix R is reduced to upper bidiagonal form BD by an orthogonal transformation:
where Q and P are orthogonal and BD is an upper bidiagonal matrix. The fast Ralha-Barlow
one-sided method is also used for this purpose (see [Ralha:2003] [Barlow_etal:2005] [Bosner_Barlow:2007]).
This two-step reduction algorithm will be more efficient if m is much larger than n.
In both the one-step and two-step algorithms, the singular values SIGMA of the bidiagonal matrix BD, which are also the singular values of MAT,
are then computed by a bisection algorithm (see [Golub_VanLoan:1996]; Sec.8.5 ). The bisection
method is applied (implicitly) to the associated min(m,n)-by-min(m,n) symmetric tridiagonal matrix
whose eigenvalues are the squares of the singular values of BD by using the differential stationary
form of the qd algorithm of Rutishauser (see [Fernando:1998]; Sec.3.1 ).
The routine outputs (parts of) SIGMA, Q and optionally P (in packed form) and
BD for a given matrix MAT. If the two-step algorithm is used, the routine outputs also O explicitly or in a packed form.
SIGMA, Q, P and BD (and also O if the two-step algorithm is selected) may then be used to obtain selected
singular vectors with subroutines bd_inviter2() or bd_deflate2().
select_singval_cmp4() is faster than select_singval_cmp3(), but is slightly less accurate.
Synopsis:
call select_singval_cmp4( mat(:m,:n) , nsing , s(:n) , failure , sort=sort , mul_size=mul_size , vector=vector , abstol=abstol , ls=ls , theta=theta , d=d(:n) , e=e(:n) , p=p(:n,:n) , gen_p=gen_p , scaling=scaling , init=init , failure_bd=failure_bd ) call select_singval_cmp4( mat(:m,:n) , rlmat(:min(m,n),:min(m,n)) , nsing , s(:n) , failure , sort=sort , mul_size=mul_size , vector=vector , abstol=abstol , ls=ls , theta=theta , d=d(:n) , e=e(:n) , tauo=tauo(:min(m,n)) , p=p(:n,:n) , gen_p=gen_p , scaling=scaling , init=init , failure_bd=failure_bd )
Examples:
ex1_select_singval_cmp4_bis.F90
ex2_select_singval_cmp4_bis.F90
-
singval_sort()¶
Purpose:
Given the singular values as output from bd_svd(), bd_svd2(), svd_cmp(),
svd_cmp2() or svd_cmp3(), singval_sort() sorts the singular values into ascending or
descending order.
Synopsis:
call singval_sort( sort , d(:n) )
-
singvec_sort()¶
Purpose:
Given the singular values and (left or right) vectors as output from bd_svd(), bd_svd2(), svd_cmp(),
svd_cmp2() or svd_cmp3(), singvec_sort() sorts the singular values into ascending or
descending order and reorders the associated singular vectors accordingly.
Synopsis:
call singvec_sort( sort , d(:n) , u(:,:n) )
-
svd_sort()¶
Purpose:
Given the singular values and the associated left and right singular vectors as output from bd_svd(),
svd_cmp(), svd_cmp2() or svd_cmp3(),
svd_sort() sorts the singular values into ascending or descending order, and, rearranges the left and
right singular vectors correspondingly.
Synopsis:
call svd_sort( sort , d(:n) , u(:,:n) , v(:,:n) ) call svd_sort( sort , d(:n) , u(:,:n) ) call svd_sort( sort , d(:n) )
-
svd_sort2()¶
Purpose:
Given the singular values and the associated left and right singular vectors as output from bd_svd2()
or svd_cmp2(), svd_sort2() sorts the singular values into ascending or descending order, and,
rearranges the left and right singular vectors correspondingly.
Synopsis:
call svd_sort2( sort , d(:n) , u(:,:n) , vt(:n,:) ) call svd_sort2( sort , d(:n) , u(:,:n) ) call svd_sort2( sort , d(:n) )
-
maxdiag_gkinv_qr()¶
Purpose:
maxdiag_gkinv_qr() computes the index of the element of maximum absolute value in the diagonal entries of
where GK is a n-by-n symmetric tridiagonal matrix with a zero diagonal,
I is the identity matrix and lambda is a scalar.
The diagonal entries of ( GK - lambda * I )-1 are computed by means of the QR
factorization of GK - lambda * I.
For more details, see [Bini_etal:2005].
It is assumed that GK is unreduced, but no check is done in the subroutine to verify
this assumption.
Synopsis:
maxdiag_gkinv = maxdiag_gkinv_qr( e(:) , lambda )
-
maxdiag_gkinv_ldu()¶
Purpose:
maxdiag_gkinv_ldu() computes the index of the element of maximum absolute value in the diagonal entries of
where GK is a n-by-n symmetric tridiagonal matrix with a zero diagonal,
I is the identity matrix and lambda is a scalar.
The diagonal entries of ( GK - lambda * I )-1 are computed by means of LDU and UDL
factorization of GK - lambda * I.
For more details, see [Fernando:1997].
It is assumed that GK is unreduced, but no check is done in the subroutine to verify
this assumption.
Synopsis:
maxdiag_gkinv = maxdiag_gkinv_ldu( e(:) , lambda )
-
gk_qr_cmp()¶
Purpose:
gk_qr_cmp() factorizes the symmetric matrix GK - lambda * I, where
GK is an n-by-n symmetric tridiagonal matrix with a zero diagonal,
I is the identity matrix and lambda is a scalar. as
where Q is an orthogonal matrix represented as the product of n-1 Givens
rotations and R is an upper triangular matrix with at most two non-zero
super-diagonal elements per column.
The parameter lambda is included in the routine so that gk_qr_cmp() may
be used to obtain eigenvectors of GK by inverse iteration.
The subroutine also computes the index of the entry of maximum absolute value
in the diagonal of ( GK - lambda * I )-1, which provides a good initial
approximation to start the inverse iteration process for computing the eigenvector
associated with the eigenvalue lambda.
For further details, see [Bini_etal:2005] [Fernando:1997] [Parlett_Dhillon:1997].
Synopsis:
call gk_qr_cmp( e(:n-1) , lambda , cs(:n-1) , sn(:n-1) , diag(:n) , sup1(:n) , sup2(:n) , maxdiag_gkinv )
-
bd_inviter()¶
Purpose:
bd_inviter() computes the left and right singular vectors of a real n-by-n bidiagonal
matrix BD corresponding to specified singular values, using Fernando’s method and
inverse iteration on the Tridiagonal Golub-Kahan (TGK) form of the bidiagonal matrix BD.
The singular values used as input of bd_inviter() can be computed with a call to bd_svd(),
bd_singval() or bd_singval2().
Moreover, the singular values used as input of bd_inviter() can be computed to high accuracy
with a call to bd_singval() or bd_singval2() with the optional
parameter ABSTOL set to sqrt(lamch("S")) for more robust results.
See description of bd_singval() or bd_singval2() for more details.
Synopsis:
call bd_inviter( upper , d(:n) , e(:n) , s , leftvec(:n) , rightvec(:n) , failure , maxiter=maxiter , scaling=scaling , initvec=initvec ) call bd_inviter( upper , d(:n) , e(:n) , s(:p) , leftvec(:n,:p) , rightvec(:n,:p) , failure , maxiter=maxiter , ortho=ortho , backward_sweep=backward_sweep , scaling=scaling , initvec=initvec )
Exemples:
-
bd_inviter2()¶
Purpose:
bd_inviter2() computes the left and right singular vectors of a full real m-by-n
matrix MAT corresponding to specified singular values, using inverse iteration.
It is required that the original matrix MAT has been first reduced to upper or lower
bidiagonal form BD by an orthogonal transformation:
where Q and P are orthogonal, and that selected singular values of BD have been computed.
These first steps can be performed in several ways:
- with a call to subroutine
select_singval_cmp()orselect_singval_cmp2()(with parameters D, E, TAUQ and TAUP), which reduce the input matrixMATwith an one-step Golub-Kahan bidiagonalisation algorithm and compute (selected) singular values of the resulting bidiagonal matrixBD; - with a call to subroutine
select_singval_cmp()orselect_singval_cmp2()(with parameters D, E, TAUQ, TAUP, RLMAT and TAUO), which reduce the input matrixMATwith a two-step Golub-Kahan bidiagonalisation algorithm and compute (selected) singular values of the resulting bidiagonal matrixBD; - using first, an one-step bidiagonalisation Golub-Kahan algorithm, with a call to
bd_cmp()(with parameters D, E, TAUQ and TAUP) followed by a call tobd_svd(),bd_singval()orbd_singval2()for computing (selected) singular values of the resulting bidiagonal matrixBD(this is equivalent of using subroutinesselect_singval_cmp()orselect_singval_cmp2()above with parameters D, E, TAUQ and TAUP); - using first, a two-step bidiagonalisation Golub-Kahan algorithm, with a call to
bd_cmp()(with parameters D, E, TAUQ, TAUP, RLMAT and TAUO ) followed by a call tobd_svd(),bd_singval()orbd_singval2()for computing (selected) singular values of the resulting bidiagonal matrixBD(this is equivalent of using subroutinesselect_singval_cmp()orselect_singval_cmp2()above with parameters D, E, TAUQ, TAUP, RLMAT and TAUO).
If m>=n, these first steps can also be performed:
- with a call to subroutine
select_singval_cmp3()orselect_singval_cmp4()(with parameters D, E and P), which reduce the input matrixMATwith an one-step Ralha-Barlow bidiagonalisation algorithm and compute (selected) singular values of the resulting bidiagonal matrixBD. - with a call to subroutine
select_singval_cmp3()orselect_singval_cmp4()(with parameters D, E, P, RLMAT and TAUO), which reduce the input matrixMATwith a two-step Ralha-Barlow bidiagonalisation algorithm and compute (selected) singular values of the resulting bidiagonal matrixBD. - using first, a one-step Ralha-Barlow bidiagonalisation algorithm, with a call to
bd_cmp2()(with parameters D, E and P), followed by a call tobd_svd(),bd_singval()orbd_singval2()for computing (selected) singular values of the resulting bidiagonal matrixBD(this is equivalent of using subroutinesselect_singval_cmp3()orselect_singval_cmp4()above with parameters D, E and P).
If max(m,n) is much larger than min(m,n), it is more efficient to use a two-step bidiagonalisation algorithm than a one-step
algorithm. Moreover, if m>=n, using the Ralha-Barlow bidiagonalisation method will be a faster method.
Once (selected) singular values of BD, which are also singular values of MAT, have been computed
by using one of the above paths, a call to bd_inviter2() will compute the associated singular vectors of MAT
if the appropriate parameters TAUQ, TAUP, P, TAUO, RLMAT and TAUO (depending on the previous selected path)
are specified in the call to bd_inviter2().
Moreover, independently of the selected paths, note that the singular values used as input of bd_inviter2() can
be computed to high accuracy, for more robust results, if the optional parameter ABSTOL set to sqrt(lamch("S"))
is used in the preliminary calls to select_singval_cmp(), select_singval_cmp2(), select_singval_cmp3(),
select_singval_cmp4(), bd_singval() or bd_singval2(), which compute the singular values of BD
(and MAT). See, for example, the description of bd_singval() or bd_singval2() for more details.
Synopsis:
call bd_inviter2( mat(:m,:n) , tauq(:min(m,n)) , taup(:min(m,n)) , d(:min(m,n)) , e(:min(m,n)) , s(:p) , leftvec(:m,:p) , rightvec(:n,:p) , failure, maxiter=maxiter , ortho=ortho , backward_sweep=backward_sweep , scaling=scaling , initvec=initvec ) call bd_inviter2( mat(:m,:n) , p(:n,:n) , d(:n) , e(:n) , s(:p) , leftvec(:m,:p) , rightvec(:n,:p) , failure, maxiter=maxiter , ortho=ortho , backward_sweep=backward_sweep , scaling=scaling , initvec=initvec ) call bd_inviter2( mat(:m,:n) , tauq(:min(m,n)) , taup(:min(m,n)) , rlmat(:min(m,n),:min(m,n)) , d(:min(m,n)) , e(:min(m,n)) , s(:p) , leftvec(:m,:p) , rightvec(:n,:p) , failure, tauo=tauo(:min(m,n)) , maxiter=maxiter , ortho=ortho , backward_sweep=backward_sweep , scaling=scaling , initvec=initvec ) call bd_inviter2( mat(:m,:n) , rlmat(:min(m,n),:min(m,n)) , p(:n,:n) , d(:n) , e(:n) , s(:p) , leftvec(:m,:p) , rightvec(:n,:p) , failure, tauo=tauo(:min(m,n)) , maxiter=maxiter , ortho=ortho , backward_sweep=backward_sweep , scaling=scaling , initvec=initvec )
Exemples:
ex1_select_singval_cmp3_bis.F90
ex1_select_singval_cmp4_bis.F90
-
upper_bd_dsqd()¶
Purpose:
upper_bd_dsqd() computes:
- the
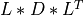 factorization of the matrix
factorization of the matrix 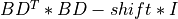 , if FLIP=
, if FLIP=false; - the
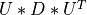 factorization of the matrix
factorization of the matrix 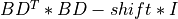 , if FLIP=
, if FLIP=true;
for a n-by-n (upper) bidiagonal matrix BD and a given scalar shift. L and U are, respectively,
unit lower and unit upper bidiagonal matrices and D is a diagonal matrix.
The differential form of the stationary QD algorithm of Rutishauser is used to compute the factorization. See [Fernando:1998] for further details.
The subroutine outputs the diagonal matrix D of the factorization, the off-diagonal
entries of L (or of U if FLIP=true) and the auxiliary variable T
in the differential form of the stationary QD algorithm.
Synopsis:
call upper_bd_dsqd( a(:n) , b(:n-1) , shift , flip , d(:n) ) call upper_bd_dsqd( a(:n) , b(:n-1) , shift , flip , d(:n) , t(:n) ) call upper_bd_dsqd( a(:n) , b(:n-1) , shift , flip , d(:n) , t(:n) , l(:n-1) )
-
upper_bd_dpqd()¶
Purpose:
upper_bd_dpqd() computes:
- the
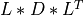 factorization of the matrix
factorization of the matrix 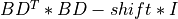 , if FLIP=
, if FLIP=false; - the
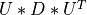 factorization of the matrix
factorization of the matrix 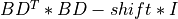 , if FLIP=
, if FLIP=true;
for a n-by-n (upper) bidiagonal matrix BD and a given scalar shift. L and U are, respectively,
unit lower and unit upper bidiagonal matrices and D is a diagonal matrix.
The differential form of the progressive QD algorithm of Rutishauser is used to compute the factorization (see [Fernando:1998] for further details).
The subroutine outputs the diagonal matrix D of the factorization, the off-diagonal
entries of L (or of U if FLIP=true) and the auxiliary variable S
in the differential form of the progressive QD algorithm.
Synopsis:
call upper_bd_dpqd( a(:n) , b(:n-1) , shift , flip , d(:n) ) call upper_bd_dpqd( a(:n) , b(:n-1) , shift , flip , d(:n) , s(:n) ) call upper_bd_dpqd( a(:n) , b(:n-1) , shift , flip , d(:n) , s(:n) , l(:n-1) )
-
upper_bd_dsqd2()¶
Purpose:
upper_bd_dsqd2() computes:
- the
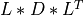 factorization of the matrix
factorization of the matrix 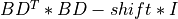 , if FLIP=
, if FLIP=false; - the
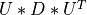 factorization of the matrix
factorization of the matrix 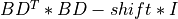 , if FLIP=
, if FLIP=true;
for a n-by-n (upper) bidiagonal matrix BD and a given scalar shift. L and U are, respectively,
unit lower and unit upper bidiagonal matrices and D is a diagonal matrix.
The differential form of the stationary QD algorithm of Rutishauser is used to compute
the factorization from the squared elements of the bidiagonal matrix BD.
See [Fernando:1998] for further details.
The subroutine outputs the diagonal matrix D of the factorization and the auxiliary
variable T (at the user option) in the differential form of the stationary QD algorithm.
Synopsis:
call upper_bd_dsqd2( q2(:n) , e2(:n-1) , shift , flip , d(:n) ) call upper_bd_dsqd2( q2(:n) , e2(:n-1) , shift , flip , d(:n) , t(:n) )
-
upper_bd_dpqd2()¶
Purpose:
upper_bd_dpqd2() computes:
- the
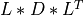 factorization of the matrix
factorization of the matrix 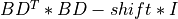 , if FLIP=
, if FLIP=false; - the
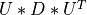 factorization of the matrix
factorization of the matrix 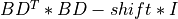 , if FLIP=
, if FLIP=true;
for a n-by-n (upper) bidiagonal matrix BD and a given scalar shift. L and U are, respectively,
unit lower and unit upper bidiagonal matrices and D is a diagonal matrix.
The differential form of the progressive QD algorithm of Rutishauser is used to compute
the factorization from the squared elements of the bidiagonal matrix BD.
See [Fernando:1998] for further details.
The subroutine outputs the diagonal matrix D of the factorization and the auxiliary
variable S in the differential form of the progressive QD algorithm.
Synopsis:
call upper_bd_dpqd2( q2(:n) , e2(:n-1) , shift , flip , d(:n) ) call upper_bd_dpqd2( q2(:n) , e2(:n-1) , shift , flip , d(:n) , s(:n) )
-
dflgen_bd()¶
Purpose:
dflgen_bd() computes deflation parameters (e.g. two chains of Givens rotations) for
a n-by-n (upper) bidiagonal matrix BD and a given singular value of BD.
On output, the arguments CS_LEFT, SN_LEFT, CS_RIGHT and SN_RIGHT contain, respectively,
the vectors of the cosines and sines coefficients of the chain of n-1 planar rotations that
deflates the real n-by-n bidiagonal matrix BD corresponding to a singular value LAMBDA.
For further details, see [Godunov_etal:1993] [Malyshev:2000].
Synopsis:
call dflgen_bd( d(:n) , e(:n-1) , lambda , cs_left(:n-1) , sn_left(:n-1) , cs_right(:n-1) , sn_right(:n-1) , scaling=scaling )
-
dflgen2_bd()¶
Purpose:
dflgen2_bd() computes and applies deflation parameters (e.g. two chains of Givens rotations) for
a n-by-n (upper) bidiagonal matrix BD and a given singular value of BD.
On input:
The arguments D and E contain, respectively, the main diagonal and off-diagonal of the bidiagonal matrix, and the argument LAMBDA contains an estimate of the singular value.
On output:
The arguments D and E contain, respectively, the new main diagonal and off-diagonal of the deflated bidiagonal matrix if the argument DEFLATE is set to
true, otherwise D and E are not changed.The arguments CS_LEFT, SN_LEFT, CS_RIGHT and SN_RIGHT contain, respectively, the vectors of the cosines and sines coefficients of the chain of
n-1planar rotations that deflates the realn-by-nbidiagonal matrixBDcorresponding to the singular value LAMBDA. One chain is applied to the left ofBD(CS_LEFT, SN_LEFT) and the other is applied to the right ofBD(CS_RIGHT, SN_RIGHT).
For further details, see [Godunov_etal:1993] [Malyshev:2000].
Synopsis:
call dflgen2_bd( d(:n) , e(:n-1) , lambda , cs_left(:n-1) , sn_left(:n-1) , cs_right(:n-1) , sn_right(:n-1) , deflate , scaling=scaling )
-
dflapp_bd()¶
Purpose:
dflapp_bd() deflates a real n-by-n (upper) bidiagonal matrix BD by two chains
of planar rotations produced by dflgen_bd() or dflgen2_bd().
On entry, the arguments D and E contain, respectively, the main diagonal and off-diagonal of the bidiagonal matrix.
On output, the arguments D and E contain, respectively, the new main diagonal
and off-diagonal of the deflated bidiagonal matrix if the argument DEFLATE is set
to true on output of dflapp_bd().
For further details, see [Godunov_etal:1993] [Malyshev:2000].
Synopsis:
call dflapp_bd( d(:n) , e(:n-1) , cs_left(:n-1) , sn_left(:n-1) , cs_right(:n-1) , sn_right(:n-1) , deflate )
-
qrstep_bd()¶
Purpose:
qrstep_bd() performs one QR step with a given shift LAMBDA on a n-by-n real (upper)
bidiagonal matrix BD.
On entry, the arguments D and E contain, respectively, the main diagonal and off-diagonal of the bidiagonal matrix.
On output, the arguments D and E contain, respectively, the new main diagonal
and off-diagonal of the deflated bidiagonal matrix if the logical argument DEFLATE is
set to true on exit or if the optional logical argument UPDATE_BD is used with the
value true on entry; otherwise the arguments D and E are not modified.
The two chains of n-1 planar rotations produced during the QR step are saved in
the arguments CS_LEFT, SN_LEFT, CS_RIGHT, SN_RIGHT.
For further details, see [Mastronardi_etal:2006].
Synopsis:
call qrstep_bd( d(:n) , e(:n-1) , lambda , cs_left(:n-1) , sn_left(:n-1) , cs_right(:n-1) , sn_right(:n-1) , deflate, update_bd )
-
qrstep_zero_bd()¶
Purpose:
qrstep_zero_bd() performs one implicit QR step with a zero shift on a n-by-n real (upper)
bidiagonal matrix BD.
On entry, the arguments D and E contain, respectively, the main diagonal and off-diagonal of the bidiagonal matrix.
On output, the arguments D and E contain, respectively, the new main diagonal
and off-diagonal of the deflated bidiagonal matrix if the logical argument DEFLATE is
set to true on exit or if the optional logical argument UPDATE_BD is used with the
value true on entry; otherwise the arguments D and E are not modified.
The two chains of n-1 planar rotations produced during the QR step are saved in
the arguments CS_LEFT, SN_LEFT, CS_RIGHT, SN_RIGHT.
For further details, see [Demmel_Kahan:1990].
Synopsis:
call qrstep_zero_bd( d(:n) , e(:n-1) , cs_left(:n-1) , sn_left(:n-1) , cs_right(:n-1) , sn_right(:n-1) , deflate, update_bd )
-
upper_bd_deflate()¶
Purpose:
upper_bd_deflate() computes the left and right singular vectors of a real (upper) bidiagonal
matrix BD corresponding to specified singular values, using a deflation technique on the BD matrix.
upper_bd_deflate() is a low-level subroutine used by bd_deflate() and
bd_deflate2() subroutines. Its use as a stand-alone method for computing singular
vectors of a bidiagonal matrix is not recommended.
Note also that the sign of the singular vectors computed by upper_bd_deflate() is arbitrary
and not necessarily consistent between the left and right singular vectors. In order
to compute consistent singular triplets, subroutine bd_deflate() must be used instead.
Synopsis:
call upper_bd_deflate( d(:n) , e(:n-1) , singval , leftvec(:n) , rightvec(:n) , failure , max_qr_steps=max_qr_steps , scaling=scaling ) call upper_bd_deflate( d(:n) , e(:n-1) , singval(:p) , leftvec(:n,:p) , rightvec(:n,:p) , failure , max_qr_steps=max_qr_steps , scaling=scaling )
-
bd_deflate()¶
Purpose:
bd_deflate() computes the left and right singular vectors of a real n-by-n bidiagonal
matrix BD corresponding to specified singular values, using deflation techniques on
the bidiagonal matrix BD.
It is highly recommended that the singular values used as input of bd_deflate() have been computed to high accuracy
with a call to bd_singval() or bd_singval2() with the optional
parameter ABSTOL set to sqrt(lamch("S")).
See description of bd_singval() or bd_singval2() for more details.
Synopsis:
call bd_deflate( upper , d(:n) , e(:n) , s(:p) , leftvec(:n,:p) , rightvec(:n,:p) , failure , max_qr_steps=max_qr_steps , ortho=ortho , scaling=scaling , inviter=inviter )
Examples:
-
bd_deflate2()¶
Purpose:
bd_deflate2() computes the left and right singular vectors of a full real m-by-n
matrix MAT corresponding to specified singular values, using deflation techniques.
It is required that the original matrix MAT has been first reduced to upper or lower
bidiagonal form BD by an orthogonal transformation:
where Q and P are orthogonal, and that selected singular values of BD have been computed.
These first steps can be performed in several ways:
- with a call to subroutine
select_singval_cmp()orselect_singval_cmp2()(with parameters D, E, TAUQ and TAUP), which reduce the input matrixMATwith an one-step Golub-Kahan bidiagonalisation algorithm and compute (selected) singular values of the resulting bidiagonal matrixBD; - with a call to subroutine
select_singval_cmp()orselect_singval_cmp2()(with parameters D, E, TAUQ, TAUP, RLMAT and TAUO), which reduce the input matrixMATwith a two-step Golub-Kahan bidiagonalisation algorithm and compute (selected) singular values of the resulting bidiagonal matrixBD; - using first, an one-step bidiagonalisation Golub-Kahan algorithm, with a call to
bd_cmp()(with parameters D, E, TAUQ and TAUP) followed by a call tobd_svd(),bd_singval()orbd_singval2()for computing (selected) singular values of the resulting bidiagonal matrixBD(this is equivalent of using subroutinesselect_singval_cmp()orselect_singval_cmp2()above with parameters D, E, TAUQ and TAUP); - using first, a two-step bidiagonalisation Golub-Kahan algorithm, with a call to
bd_cmp()(with parameters D, E, TAUQ, TAUP, RLMAT and TAUO ) followed by a call tobd_svd(),bd_singval()orbd_singval2()for computing (selected) singular values of the resulting bidiagonal matrixBD(this is equivalent of using subroutinesselect_singval_cmp()orselect_singval_cmp2()above with parameters D, E, TAUQ, TAUP, RLMAT and TAUO).
If m>=n, these first steps can also be performed:
- with a call to subroutine
select_singval_cmp3()orselect_singval_cmp4()(with parameters D, E and P), which reduce the input matrixMATwith an one-step Ralha-Barlow bidiagonalisation algorithm and compute (selected) singular values of the resulting bidiagonal matrixBD. - with a call to subroutine
select_singval_cmp3()orselect_singval_cmp4()(with parameters D, E, P, RLMAT and TAUO), which reduce the input matrixMATwith a two-step Ralha-Barlow bidiagonalisation algorithm and compute (selected) singular values of the resulting bidiagonal matrixBD. - using first, a one-step Ralha-Barlow bidiagonalisation algorithm, with a call to
bd_cmp2()(with parameters D, E and P), followed by a call tobd_svd(),bd_singval()orbd_singval2()for computing (selected) singular values of the resulting bidiagonal matrixBD(this is equivalent of using subroutinesselect_singval_cmp3()orselect_singval_cmp4()above with parameters D, E and P).
If max(m,n) is much larger than min(m,n), it is more efficient to use a two-step bidiagonalisation algorithm than a one-step
algorithm. Moreover, if m>=n, using the Ralha-Barlow bidiagonalisation method will be a faster method.
Once (selected) singular values of BD, which are also singular values of MAT, have been computed
by using one of the above paths, a call to bd_deflate2() will compute the associated singular vectors of MAT
if the appropriate parameters TAUQ, TAUP, P, TAUO, RLMAT and TAUO (depending on the previous selected path)
are specified in the call to bd_deflate2().
Moreover, independently of the selected paths, It is also highly recommended that the singular values used as input of bd_deflate2()
have been computed to high accuracy, for more robust results, with the optional parameter ABSTOL set to sqrt(lamch("S"))
in the preliminary calls to select_singval_cmp(), select_singval_cmp2(), select_singval_cmp3(),
select_singval_cmp4(), bd_singval() or bd_singval2(), which compute the singular values of BD
(and MAT). See, for example, the description of bd_singval() or bd_singval2() for more details.
Synopsis:
call bd_deflate2( mat(:m,:n) , tauq(:min(m,n)) , taup(:min(m,n)) , d(:min(m,n)) , e(:min(m,n)) , s(:p) , leftvec(:m,:p) , rightvec(:n,:p) , failure , max_qr_steps=max_qr_steps , ortho=ortho , scaling=scaling , inviter=inviter ) call bd_deflate2( mat(:m,:n) , p(:n,:n) , d(:n) , e(:n) , s(:p) , leftvec(:m,:p) , rightvec(:n,:p) , failure , max_qr_steps=max_qr_steps , ortho=ortho , scaling=scaling , inviter=inviter ) call bd_deflate2( mat(:m,:n) , tauq(:min(m,n)) , taup(:min(m,n)) , rlmat(:min(m,n),:min(m,n)) , d(:min(m,n)) , e(:min(m,n)) , s(:p) , leftvec(:m,:p) , rightvec(:n,:p) , failure , tauo=tauo(:min(m,n)) , max_qr_steps=max_qr_steps , ortho=ortho , scaling=scaling , inviter=inviter ) call bd_deflate2( mat(:m,:n) , rlmat(:min(m,n),:min(m,n)) , p(:n,:n) , d(:n) , e(:n) , s(:p) , leftvec(:m,:p) , rightvec(:n,:p) , failure , tauo=tauo(:min(m,n)) , max_qr_steps=max_qr_steps , ortho=ortho , scaling=scaling , inviter=inviter )
Examples:
ex2_select_singval_cmp3_bis.F90
ex2_select_singval_cmp4_bis.F90
-
product_svd_cmp()¶
Purpose:
product_svd_cmp() computes the singular value decomposition of the product of a
m-by-n matrix A by the transpose of a p-by-n matrix B:
where A and B have more rows than columns ( n<=:data:min(m,p) ), SIGMA is an n-by-n matrix
which is zero except for its diagonal elements, U is an m-by-n orthogonal
matrix, and V is an p-by-n orthogonal matrix. The diagonal elements of SIGMA
are the singular values of A * BT; they are real and non-negative.
The columns of U and V are the left and right singular vectors
of A * BT, respectively.
Synopsis:
call product_svd_cmp( a(:m,:n) , b(:p,:n) , s(:n) , failure , sort=sort , maxiter=maxiter , max_francis_steps=max_francis_step , perfect_shift=perfect_shift )
-
ginv()¶
Purpose:
ginv() returns the generalized (e.g. Moore-Penrose) inverse MAT+ of a m-by-n real matrix, MAT.
The generalized inverse of MAT is a n-by-m matrix and is computed with the help of the SVD of MAT [Golub_VanLoan:1996].
Synopsis:
matginv(:n,:m) = ginv( mat(:m,:n) , tol=tol , maxiter=maxiter , max_francis_steps=max_francis_step , perfect_shift=perfect_shift )
Exemples:
-
comp_ginv()¶
Purpose:
comp_ginv() computes the generalized (e.g. Moore-Penrose) inverse MAT+ of a m-by-n real matrix, MAT.
The generalized inverse of MAT is a n-by-m matrix and is computed with the help of the SVD of MAT [Golub_VanLoan:1996].
Synopsis:
call comp_ginv( mat(:m,:n) , failure, matginv(:n,:m), tol=tol , singvalues=singvalues(:min(m,n)) , krank=krank , mul_size=mul_size , maxiter=maxiter , max_francis_steps=max_francis_step , perfect_shift=perfect_shift ) call comp_ginv( mat(:m,:n) , failure , tol=tol , singvalues=singvalues(:min(m,n)) , krank=krank , mul_size=mul_size , maxiter=maxiter , max_francis_steps=max_francis_step , perfect_shift=perfect_shift )
Exemples:
-
gen_bd_mat()¶
Purpose:
gen_bd_mat() generates different types of bidiagonal matrices with known singular values or specific numerical properties such as clustered singular values for testing purposes of singular value decomposition bidiagonal solvers.
Optionally, the singular values of the selected bidiagonal matrix can be computed analytically, if possible, or by a bisection algorithm with high absolute and relative accuracies.
Synopsis:
call gen_bd_mat( type , d(:n) , e(:n) , failure=failure , known_singval=known_singval , from_tridiag=from_tridiag , singval=singval(:n) , sort=sort , val1=val1 , val2=val2 , l0=l0 , glu0=glu0 )