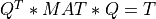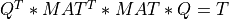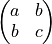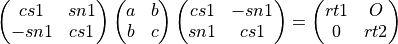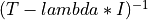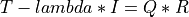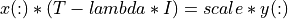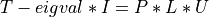MODULE Eig_Procedures¶
Module EIG_Procedures exports a large set of procedures for computing (selected) eigenvalues and/or (selected) eigenvectors of a symmetric (tridiagonal) matrix [Lawson_Hanson:1974] [Golub_VanLoan:1996] [Parlett:1998]. Fast methods for obtaining approximations of a truncated EigenValue Decomposition (EVD) of symmetric matrices based on randomization algorithms are also included [Halko_etal:2011].
The standard real symmetric eigenvalue problem is to find eigenvalues 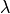 and eigenvectors
and eigenvectors 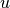 such that
such that
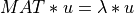
where MAT is a n-by-n real symmetric matrix.
For an input n-by-n dense matrix MAT, this module provides routines for:
the transformation of
MATto tridiagonal formT,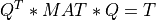
where
Qis an-by-northogonal matrix;the computation of the eigenvalues
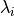 and eigenvectors
and eigenvectors 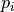 of
of T,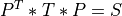
where
Sis an-by-ndiagonal matrix with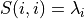 and
and Pis then-by-nmatrix of eigenvectors ofT;the back-transformation of the eigenvectors
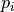 of
of Tto eigenvectors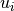 of
of MAT,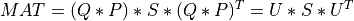
where
Uis then-by-nmatrix of eigenvectors ofMATand the eigenvalues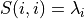 of
of Tare also the eigenvalues ofMAT.
The transformation of MAT to tridiagonal form T, the generation of the associated orthogonal factor Q, the computation of the eigenvectors
of T and the back-transformation the eigenvectors of T to eigenvectors of MAT are done with multi-threaded and blocked
algorithms [Dongarra_etal:1989] [Golub_VanLoan:1996] [Walker:1988]. All algorithms are parallelized with OpenMP [openmp].
Depending on the situation and the algorithm used, it is also possible to compute selected, or only the largest or smallest eigenvalues
and the associated eigenvectors.
Currently, STATPACK includes four different algorithms for computing (selected) eigenvalues of a tridiagonal matrix T:
- the implicit QR method [Lawson_Hanson:1974] [Golub_VanLoan:1996] [Parlett:1998] ;
- the fast Pal-Walker-Kahan variant of the implicit QR method, which does not used square roots [Parlett:1998] ;
- the bisection method, which is based on Sturm sequences and requires
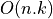 operations to compute
operations to compute keigenvalues ofT[Golub_VanLoan:1996] [Parlett:1998] ; - and a rational QR algorithm, where the shift is determined using Newton’s method and makes it possible to steer the iteration toward desired eigenvalues [Reinsch_Bauer:1968]. This method also allows computation of subset of eigenvalues.
These STATPACK eigenvalues routines generally compute eigenvalues of T (or MAT) to an absolute accuracy of 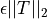 (or
(or 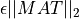 ), where
), where  is the machine precision. If higher accuracy is wanted, subroutine
is the machine precision. If higher accuracy is wanted, subroutine symtrid_bisect()
(or select_eigval_cmp3() in case of a dense matrix MAT) should be used with the optional argument ABSTOL set to sqrt(lamch("S")).
Currently, STATPACK includes three different methods for computing eigenvectors of a tridiagonal matrix T:
- implicit QR iteration [Golub_VanLoan:1996] [Parlett:1998];
- inverse iteration combined with Fernando’s method [Golub_VanLoan:1996] [Ipsen:1997] [Dhillon:1998] [Fernando:1997] [Bini_etal:2005];
- and a deflation algorithm inspired from the work of Godunov and collaborators, which is also related to Fernando’s method for computing eigenvectors [Godunov_etal:1993] [Malyshev:2000] and [Fernando:1997].
The implicit QR algorithm applies a sequence of similarity transformations to the tridiagonal matrix T until its off-diagonal elements
become negligible and the diagonal elements have converged to the eigenvalues of T [Golub_VanLoan:1996]. It consists of a bulge-chasing
procedure that implicitly includes shifts and use plane rotations (e.g. Givens rotations) which preserve the tridiagonal form of T.
High performance is obtained by restructuring the QR Algorithm with a wave-front algorithm to accumulate the Givens rotations for
computing the eigenvectors [VanZee_etal:2011], by the use of a novel perfect shift strategy in the QR iterations inspired by the works of [Godunov_etal:1993] [Malyshev:2000] and [Fernando:1997] and, finally, OpenMP parallelization [Demmel_etal:1993]. Subset computations are not possible with the QR algorithm, but it is possible to
compute only all the eigenvalues or both all the eigenvalues and associated eigenvectors.
If the distance between the eigenvalues of T is sufficient relative to the norm of T, then computing eigenvectors
by inverse iteration is a 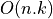 process, where
process, where k is the number of eigenvectors to compute [Ipsen:1997] [Dhillon:1998].
However, if the eigenvalues of T are too close, the eigenvectors must be orthogonalized by the modified Gram-Schmidt algorithm, which is
much more expensive.
The deflation method combines Fernando’s method for the computation of eigenvectors [Fernando:1997] [Parlett_Dhillon:1997] with deflation procedures
by Givens rotations, see [Godunov_etal:1993] [Parlett_Dhillon:1997] [Malyshev:2000] for more details. QR iterations with a perfect shift strategy
are also used as a back-up procedure if the deflation technique fails [Mastronardi_etal:2006]. If the eigenvalues are well-separated, the deflation
method is also a 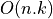 process, where
process, where k is the number of eigenvectors to compute. It is highly recommended to compute the eigenvalues
to high accuracy (e.g. with symtrid_bisect() or select_eigval_cmp3()) for the success of the deflation technique.
Parallelism concerns only the computation of eigenvectors in the QR method, but both the computation of the eigenvalues and the eigenvectors in the bisection-inverse iteration and bisection-deflation methods.
Finally, as explained above, subset computations are not possible in the standard implicit QR algorithm, but is possible with the two other
methods for computing eigenvectors and for the bisection method for computing eigenvalues. The m largest or smallest eigenvalues of
a symmetric n-by-n tridiagonal matrix T can also be computed using the rational QR method [Reinsch_Bauer:1968].
This rational QR method is sequential.
The driver and computational routines provided in this module are different from the corresponding routines provided by LAPACK [Anderson_etal:1999] and are (much) faster if OpenMP and BLAS support are used, but less accurate for the same precision.
In addition to these standard and accurate driver and computational routines based on implicit QR tridiagonal, inverse or deflation iterations applied to tridiagonal matrices after a preliminary tridiagonal reduction step, module Eig_Procedures also includes a routine for computing an approximation of the largest eigenvalues (in absolute magnitude) and associated eigenvectors of full symmetric matrices using randomized power, subspace or block Krylov iterations [Halko_etal:2011] [Musco_Musco:2015] [Martinsson:2019]. Note also that module SVD_Procedures contains a similar routine, reig_pos_cmp(), for real symmetric positive (semi-)definite matrices based on the so-called Nystrom method [Halko_etal:2011] [Martinsson:2019]. The Nystrom method provides more accurate results for positive semi-definite matrices. For a good introduction to randomized linear algebra, see [Li_etal:2017], [Martinsson:2019] and [Erichson_etal:2019].
These randomized methods identify a subspace that captures most of the action (i.e. capture the largest singular values) of the symmetric matrix. The basic idea of these randomized methods is to use random projection to approximate the dominant subspace of a (symmetric) matrix.The input (symmetric) matrix is then compressed-either explicitly or implicitly-to this subspace, and the reduced symmetric matrix is manipulated inexpensively by standard methods to obtain the desired low-rank factorization. In many cases, this approach beats largely its classical competitors in terms of speed [Halko_etal:2011] [Musco_Musco:2015] [Li_etal:2017]. Thus, these routines based on recent randomized algorithms are much faster than the standard drivers included in module Eig_Procedures for computing truncated EVD of a symmetric matrix. Yet, such randomized methods are also shown to compute with a very high probability low-rank approximations that are accurate, and are known to perform even better in many practical situations when the eigenvalues of the input symmetric matrix decay quickly [Halko_etal:2011] [Li_etal:2017].
The randomized algorithms are also parallelized with OpenMP [openmp].
Please note that driver and computational routines provided in this module apply only to real data of kind stnd. The real kind type stnd is defined in module Select_Parameters. Computation of eigenvalues and eigenvectors for a complex matrix are not provided in this release of STATPACK.
In order to use one of these routines, you must include an appropriate use Eig_Procedures or use Statpack statement
in your Fortran program, like:
use EIG_Procedures, only: eig_cmp
or :
use Statpack, only: eig_cmp
Here is the list of the public routines exported by module EIG_Procedures:
-
symtrid_cmp()¶
Purpose:
symtrid_cmp() reduces a real n-by-n symmetric matrix MAT (eventually
stored in in packed form) to symmetric tridiagonal form T by an
orthogonal similarity transformation:
The transformation to tridiagonal form T, which use Householder reflectors, is blocked and
parallelized with OpenMP if the UPPER argument is not used [Dongarra_etal:1989].
On the other hand, if the UPPER argument is used, the standard sequential and non-blocked algorithm is used [Golub_VanLoan:1996] [Parlett:1998].
Synopsis:
call symtrid_cmp( mat(:n,:n) , d(:n) , e(:n) , store_q , upper ) call symtrid_cmp( mat(:n,:n) , d(:n) , e(:n) , store_q ) call symtrid_cmp( matp(:(n*(n+1)/2)) , d(:n) , e(:n) , store_q , upper ) call symtrid_cmp( matp(:(n*(n+1)/2)) , d(:n) , e(:n) , store_q )
Examples:
-
symtrid_cmp2()¶
Purpose:
symtrid_cmp2() reduces a real n-by-n symmetric matrix cross-product
, where MAT is a m-by-n matrix, with m >= n, to symmetric tridiagonal
form T by an orthogonal similarity transformation:
where Q is an orthogonal n-by-n matrix.
symtrid_cmp2() computes T and Q, using a parallel (if OpenMP support is activated) and blocked
version of the one-sided Ralha tridiagonal reduction algorithm [Ralha:2003] [Hegland_etal:1999], without explicitly
forming the matrix cross-product 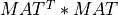 .
.
The matrix Q is stored as a product of elementary Householder reflectors in the lower triangle of MAT on exit,
if the input logical argument STORE_Q is set to the value true. Subroutines ortho_gen_symtrid() and
apply_q_symtrid() (with logical argument UPPER set to false) can then be used to generate explicitly
the orthogonal matrix Q or to apply it to an another matrix.
Synopsis:
call symtrid_cmp2( mat(:n,:n) , d(:n) , e(:n) , store_q )
Examples:
-
ortho_gen_symtrid()¶
Purpose:
ortho_gen_symtrid() generates a real orthogonal matrix Q which is defined
as the product of n-1 elementary reflectors of order n, as returned by
symtrid_cmp().
The generation of the real orthogonal matrix Q is blocked and parallelized with OpenMP
in all cases [Walker:1988].
Synopsis:
call ortho_gen_symtrid( mat(:n,:n) , upper ) call ortho_gen_symtrid( mat(:n,:n) )
Examples:
-
apply_q_symtrid()¶
Purpose:
apply_q_symtrid() overwrites the general real m-by-n matrix C with:
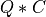 if LEFT =
if LEFT = trueand TRANS =false;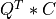 if LEFT =
if LEFT = trueand TRANS =true;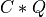 if LEFT =
if LEFT = falseand TRANS =false;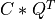 if LEFT =
if LEFT = falseand TRANS =true.
where Q is a real orthogonal matrix of order nq and is defined as the product
of nq-1 elementary reflectors
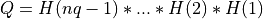 , if UPPER =
, if UPPER = trueor is not used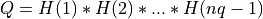 , if UPPER =
, if UPPER = false
as returned by symtrid_cmp() or symtrid_cmp2().
Q is of order m (=:data:nq) and is the product of m-1 reflectors if LEFT = true.
Q is of order n (=:data:nq) and is the product of n-1 reflectors if LEFT = false.
The procedure is is blocked and parallelized with OpenMP in all cases [Walker:1988].
Synopsis:
call apply_q_symtrid( mat(:nq,:nq) , c(:,:) , left , trans , upper ) call apply_q_symtrid( mat(:nq,:nq) , c(:,:) , left , trans ) call apply_q_symtrid( matp(:(nq*(nq+1)/2)) , c(:,:) , left , trans , upper ) call apply_q_symtrid( matp(:(nq*(nq+1)/2)) , c(:,:) , left , trans , )
The shape of C must verify:
size( C, 1 ) = nqif LEFT =truesize( C, 2 ) = nqif LEFT =false
-
symtrid_qri()¶
Purpose:
symtrid_qri() computes all eigenvalues and eigenvectors of a
symmetric n-by-n tridiagonal matrix using the implicit QR method [Golub_VanLoan:1996]
[Parlett:1998] [Greenbaum_Dongarra:1989] .
The eigenvalues and eigenvectors of a full symmetric matrix can also be found if symtrid_cmp() and
ortho_gen_symtrid() have been used to reduce this matrix to tridiagonal form.
The computation of the eigenvectors are parallelized with OpenMP [Demmel_etal:1993].
If eigenvectors are not requested, symtrid_qri() computes all eigenvalues of a symmetric tridiagonal matrix using the fast Pal-Walker-Kahan variant of the QR algorithm, which does not use square roots [Parlett:1998].
Synopsis:
call symtrid_qri( d(:n) , e(:n) , failure , mat(:n,:n) , init_mat=init_mat , sort=sort , maxiter=maxiter ) call symtrid_qri( d(:n) , e(:n) , failure , sort=sort , maxiter=maxiter )
Examples:
-
symtrid_qri2()¶
Purpose:
symtrid_qri2() computes all eigenvalues and eigenvectors of a
symmetric n-by-n tridiagonal matrix with a perfect shift strategy
for the eigenvectors [Godunov_etal:1993] [Malyshev:2000] .
If the perfect shift strategy failed for some eigenvectors, these eigenvectors are computed with the implicit QR method [Golub_VanLoan:1996] [Parlett:1998].
The eigenvalues and eigenvectors of a full symmetric matrix can also be found if symtrid_cmp() and
ortho_gen_symtrid() have been used to reduce this matrix to tridiagonal form.
Furthermore, the computation of the eigenvectors is blocked with a wave-front algorithm for applying Givens rotations [VanZee_etal:2011] and parellelized with OpenMP [Demmel_etal:1993].
If eigenvectors are not requested, symtrid_qri2() computes all eigenvalues of a symmetric tridiagonal matrix using the fast Pal-Walker-Kahan variant of the QR algorithm, which does not use square roots [Parlett:1998].
symtrid_qri2() is much faster than symtrid_qri() for computing eigenvectors of large matrices,
but may be less efficient for small matrices.
Synopsis:
call symtrid_qri2( d(:n) , e(:n) , failure , mat(:n,:n) , init_mat=init_mat , sort=sort , maxiter=maxiter, max_francis_steps=max_francis_steps ) call symtrid_qri2( d(:n) , e(:n) , failure , sort=sort , maxiter=maxiter )
Examples:
-
symtrid_qri3()¶
Purpose:
symtrid_qri3() computes all eigenvalues and eigenvectors of a
symmetric n-by-n tridiagonal matrix with the implicit QR method
[Golub_VanLoan:1996] [Parlett:1998].
The eigenvalues and eigenvectors of a full symmetric matrix can also be found if symtrid_cmp() and
ortho_gen_symtrid() have been used to reduce this matrix to tridiagonal form.
The computation of the eigenvectors is blocked with a wave-front algorithm for applying Givens rotations [VanZee_etal:2011] and parellelized with OpenMP [Demmel_etal:1993].
If eigenvectors are not requested, symtrid_qri3() computes all eigenvalues of a symmetric tridiagonal matrix using the implicit QR method [Golub_VanLoan:1996] [Parlett:1998].
symtrid_qri3() is (slightly) less faster than symtrid_qri2() for computing eigenvectors
of large matrices, but may be more robust.
Synopsis:
call symtrid_qri3( d(:n) , e(:n) , failure , mat(:n,:n) , init_mat=init_mat , sort=sort , maxiter=maxiter, max_francis_steps=max_francis_steps ) call symtrid_qri3( d(:n) , e(:n) , failure , sort=sort , maxiter=maxiter )
Examples:
-
symtrid_ratqri()¶
Purpose:
symtrid_ratqri() computes the m largest or smallest eigenvalues of a real symmetric n-by-n
tridiagonal matrix using a rational QR method [Reinsch_Bauer:1968].
The m largest or smallest eigenvalues of a full symmetric matrix can also be found
if symtrid_cmp() and ortho_gen_symtrid() have been used to reduce this matrix to tridiagonal form.
This subroutine is not parallelized, but allows computation of a subset of the eigenvalues of
a symmetric n-by-n tridiagonal matrix, a possibility, which is not offered by
symtrid_qri(), symtrid_qri2() and symtrid_qri3().
Synopsis:
call symtrid_ratqri( d(:n) , e(:n) , m , failure , small=small , tol=tol )
Examples:
-
symtrid_ratqri2()¶
Purpose:
symtrid_ratqri2() computes the largest or smallest eigenvalues of a symmetric n-by-n
tridiagonal matrix in algebraic value whose sum (e.g. sum of the absolute values of the eigenvalues) exceeds a given value.
A rational QR method is used [Reinsch_Bauer:1968].
The largest or smallest eigenvalues of a full symmetric matrix whose sum exceeds a given threshold in algebraic value
can also be found, if symtrid_cmp() and ortho_gen_symtrid() have been used to reduce this matrix
to tridiagonal form.
This subroutine is not parallelized, but allows computation of a subset of the eigenvalues of
a symmetric n-by-n tridiagonal matrix, a possibility, which is not offered by symtrid_qri(),
symtrid_qri2() and symtrid_qri3().
Synopsis:
call symtrid_ratqri2( d(:n) , e(:n) , val , failure , m , small=small , tol=tol )
Examples:
-
symtrid_bisect()¶
Purpose:
symtrid_bisect() computes all or some of the largest or smallest eigenvalues of a real n-by-n
symmetric tridiagonal matrix T using a bisection method [Golub_VanLoan:1996].
The full set, largest or smallest eigenvalues of a full symmetric matrix can also be found
if symtrid_cmp() has been used to reduce this matrix to tridiagonal form.
This subroutine is parallelized if OPENMP is used and allows the computation of eigenvalues to high (relative) accuracy if desired (e.g. with the optional argument ABSTOL).
Synopsis:
call symtrid_bisect( d(:n) , e(:n) , neig , w(:n) , failure , small=small , sort=sort , vector=vector , abstol=abstol , le=le , theta=theta , scaling=scaling , init=init )
Examples:
-
eig_cmp()¶
Purpose:
eig_cmp() computes all eigenvalues and eigenvectors of a
n-by-n real symmetric matrix MAT.
The matrix MAT is first transformed to tridiagonal form T, then the eigenvalues
and the eigenvectors are computed by the QR implicit algorithm [Golub_VanLoan:1996].
The transformation to tridiagonal form T is blocked and parallelized with OpenMP if the
UPPER argument is not used [Dongarra_etal:1989]. Otherwise, a sequential and non-blocked algorithm is used
for this transformation [Golub_VanLoan:1996] [Parlett:1998].
The computation of the eigenvectors by the QR implicit algorithm is parallelized with OpenMP in all cases [Demmel_etal:1993].
Synopsis:
call eig_cmp( mat(:n,:n) , eigval(:n) , failure , upper , sort=sort , maxiter=maxiter ) call eig_cmp( mat(:n,:n) , eigval(:n) , failure , sort=sort , maxiter=maxiter )
Examples:
-
eig_cmp2()¶
Purpose:
eig_cmp2() computes all eigenvalues and eigenvectors of a
n-by-n real symmetric matrix MAT.
The matrix MAT is first transformed to tridiagonal form T, then the eigenvalues
are computed by the Pal-Walker-Kahan variant of the QR algorithm [Parlett:1998] and the eigenvectors
are computed with a perfect shift strategy [Godunov_etal:1993] [Malyshev:2000], or the
implicit QR algorithm [Parlett:1998] if the perfect shift strategy fails. The Givens rotations, which are used
in the perfect shift strategy or the implicit QR algorithm, are accumulated with a fast wavefront
algorithm for computing the eigenvectors [VanZee_etal:2011].
The transformation to tridiagonal form T is blocked and parallelized with OpenMP if the
UPPER argument is not used [Dongarra_etal:1989]. Otherwise, a sequential and non-blocked
algorithm is used [Golub_VanLoan:1996] [Parlett:1998].
Furthermore, the computation of the eigenvectors is blocked with a wave-front algorithm for applying Givens rotations [VanZee_etal:2011] and parellelized with OpenMP in all cases [Demmel_etal:1993].
eig_cmp2() is much faster than eig_cmp() for large matrices, but may be less efficient for small matrices.
Synopsis:
call eig_cmp2( mat(:n,:n) , eigval(:n) , failure , upper , sort=sort , maxiter=maxiter , max_francis_steps=max_francis_steps ) call eig_cmp2( mat(:n,:n) , eigval(:n) , failure , sort=sort , maxiter=maxiter , max_francis_steps=max_francis_steps )
Examples:
-
eig_cmp3()¶
Purpose:
eig_cmp3() computes all eigenvalues and eigenvectors of a
n-by-n real symmetric matrix MAT.
The matrix MAT is first transformed to tridiagonal form T, then the eigenvalues/eigenvectors
are computed by the implicit QR algorithm [Parlett:1998]. The Givens rotations used in the implicit QR algorithm
are accumulated with a fast wavefront algorithm for computing the eigenvectors [VanZee_etal:2011].
The transformation to tridiagonal form T is blocked and parallelized with OpenMP if the
UPPER argument is not used [Dongarra_etal:1989]. Otherwise, a sequential and non-blocked
algorithm is used [Golub_VanLoan:1996] [Parlett:1998].
Furthermore, the computation of the eigenvectors is blocked with a wave-front algorithm for applying Givens rotations [VanZee_etal:2011] and parellelized with OpenMP [Demmel_etal:1993].
eig_cmp3() is much faster than eig_cmp() for large matrices and less faster than eig_cmp2(), but may be more robust.
Synopsis:
call eig_cmp3( mat(:n,:n) , eigval(:n) , failure , upper , sort=sort , maxiter=maxiter , max_francis_steps=max_francis_steps ) call eig_cmp3( mat(:n,:n) , eigval(:n) , failure , sort=sort , maxiter=maxiter , max_francis_steps=max_francis_steps )
Examples:
-
laev2()¶
Purpose:
laev2() computes the eigendecomposition of a 2-by-2 real symmetric matrix
On return, RT1 is the eigenvalue of larger absolute value, RT2 is the
eigenvalue of smaller absolute value, and (CS1,SN1) is the unit right
eigenvector for RT1, giving the decomposition
This subroutine is from LAPACK.
Synopsis:
call laev2( a , b , c , rt1 , rt2 , cs1 , sn1 )
-
reig_cmp()¶
Purpose:
reig_cmp() computes approximations of the neig largest eigenvalues (in absolute magnitude) and associated
eigenvectors of a full real n-by-n symmetric matrix MAT using
randomized power, subspace or block Krylov iterations [Halko_etal:2011] [Musco_Musco:2015] [Martinsson:2019].
This routine is always significantly faster than eig_cmp(), eig_cmp2(), eig_cmp3(),
trid_inviter() or trid_deflate() because of the use of very fast randomized
algorithms [Halko_etal:2011] [Gu:2015] [Musco_Musco:2015] [Martinsson:2019]. However, the computed neig
largest eigenvalues (in absolute magnitude) and associated eigenvectors are only approximations of
the true largest eigenvalues and eigenvectors.
Note that module SVD_Procedures contains a similar routine, reig_pos_cmp(), for
real symmetric positive semi-definite matrices based on the so-called Nystrom method [Halko_etal:2011] [Martinsson:2019].
The Nystrom method provides more accurate results for positive semi-definite matrices, so if your input matrix MAT is
positive semi-definite, reig_pos_cmp() is a better choice than reig_cmp().
The routine returns approximations to the first neig eigenvalues (in absolute magnitude) and
the associated eigenvectors corresponding to a partial EVD of a symmetric matrix MAT.
Synopsis:
call reig_cmp( mat(:n,:n) , eigval(:neig) , eigvec(:n,:neig) , failure=failure , niter=niter , nover=nover , ortho=ortho , extd_samp=extd_samp , rng_alg=rng_alg , maxiter=maxiter )
Examples:
-
eig_sort()¶
Purpose:
Given the eigenvalues D and, eventually, eigenvectors U as output from eig_cmp(),
eig_cmp2(), eig_cmp3(), symtrid_qri(), symtrid_qri2(), symtrid_qri3()
or other STATPACK routines which compute eigenvalues and eigenvectors, eig_sort() sorts
the eigenvalues D into ascending or descending order, and, rearranges the columns of U correspondingly.
Synopsis:
call eig_sort( sort , d(:m), u(:n,:m) ) call eig_sort( sort , d(:m) )
-
eig_abs_sort()¶
Purpose:
Given the eigenvalues D and, eventually, eigenvectors U as output from eig_cmp(),
eig_cmp2(), eig_cmp3(), symtrid_qri(), symtrid_qri2(), symtrid_qri3()
or other STATPACK routines which compute eigenvalues and eigenvectors, eig_abs_sort() sorts
the eigenvalues D into ascending or descending order of absolute magnitude, and, rearranges the
columns of U correspondingly.
Synopsis:
call eig_abs_sort( sort , d(:m), u(:n,:m) ) call eig_abs_sort( sort , d(:m) )
Examples:
-
eigvalues()¶
Purpose:
eigvalues() computes all eigenvalues of a n-by-n real symmetric matrix MAT.
The matrix MAT is first transformed to symmetric tridiagonal form T
by an orthogonal similarity transformation:
then the eigenvalues of T, which are also the eigenvalues of MAT, are computed
by the Pal-Walker-Kahan variant of the QR algorithm [Parlett:1998].
If the QR algorithm fails to converge eigvalues() returns a n-vector filled with NANs.
Synopsis:
eigval(:n) = eigvalues( mat(:n,:n) , upper , sort=sort , maxiter=maxiter ) eigval(:n) = eigvalues( mat(:n,:n) , sort=sort , maxiter=maxiter )
Examples:
-
eigval_cmp()¶
Purpose:
eigval_cmp() computes all eigenvalues of a n-by-n real symmetric matrix MAT,
eventually stored in packed form.
The matrix MAT is first transformed to symmetric tridiagonal form T
by an orthogonal similarity transformation:
then the eigenvalues of T, which are also the eigenvalues of MAT, are computed
by the Pal-Walker-Kahan variant of the QR algorithm [Parlett:1998].
Synopsis:
call eigval_cmp( mat(:n,:n) , eigval(:n) , failure , upper , sort=sort , maxiter=maxiter , d_e=d_e(:n,:2) ) call eigval_cmp( mat(:n,:n) , eigval(:n) , failure , sort=sort , maxiter=maxiter , d_e=d_e(:n,:2) ) call eigval_cmp( matp(:(n*(n+1)/2)) , eigval(:n) , failure , upper , sort=sort , maxiter=maxiter , d_e=d_e(:n,:2) ) call eigval_cmp( matp(:(n*(n+1)/2)) , eigval(:n) , failure , sort=sort , maxiter=maxiter , d_e=d_e(:n,:2) )
Examples:
-
eigval_cmp2()¶
Purpose:
eigval_cmp2() computes all eigenvalues of a n-by-n real symmetric matrix MAT,
eventually stored in packed form.
The matrix MAT is first transformed to symmetric tridiagonal form T
by an orthogonal similarity transformation:
then the eigenvalues of T, which are also the eigenvalues of MAT, are computed
by the Pal-Walker-Kahan variant of the QR algorithm [Parlett:1998].
A slightly different version of the Pal-Walker-Kahan algorithm is used compared to the
eigval_cmp() generic subroutine.
Synopsis:
call eigval_cmp2( mat(:n,:n) , eigval(:n) , failure , upper , sort=sort , maxiter=maxiter , d_e=d_e(:n,:2) ) call eigval_cmp2( mat(:n,:n) , eigval(:n) , failure , sort=sort , maxiter=maxiter , d_e=d_e(:n,:2) ) call eigval_cmp2( matp(:(n*(n+1)/2)) , eigval(:n) , failure , upper , sort=sort , maxiter=maxiter , d_e=d_e(:n,:2) ) call eigval_cmp2( matp(:(n*(n+1)/2)) , eigval(:n) , failure , sort=sort , maxiter=maxiter , d_e=d_e(:n,:2) )
Examples:
-
eigval_cmp3()¶
Purpose:
eigval_cmp3() computes all eigenvalues of a n-by-n real symmetric matrix MAT,
eventually stored in packed form.
The matrix MAT is first transformed to symmetric tridiagonal form T
by an orthogonal similarity transformation:
then the eigenvalues of T, which are also the eigenvalues of MAT, are computed
by the implicit QR algorithm [Parlett:1998] [Golub_VanLoan:1996] .
Synopsis:
call eigval_cmp3( mat(:n,:n) , eigval(:n) , failure , upper , sort=sort , maxiter=maxiter , d_e=d_e(:n,:2) ) call eigval_cmp3( mat(:n,:n) , eigval(:n) , failure , sort=sort , maxiter=maxiter , d_e=d_e(:n,:2) ) call eigval_cmp3( matp(:(n*(n+1)/2)) , eigval(:n) , failure , upper , sort=sort , maxiter=maxiter , d_e=d_e(:n,:2) ) call eigval_cmp3( matp(:(n*(n+1)/2)) , eigval(:n) , failure , sort=sort , maxiter=maxiter , d_e=d_e(:n,:2) )
Examples:
-
select_eigval_cmp()¶
Purpose:
select_eigval_cmp() computes the m = size(eigval) largest or smallest eigenvalues of
a n-by-n real symmetric matrix MAT. MAT can be stored in packed form.
The matrix MAT is first transformed to symmetric tridiagonal form T
by an orthogonal similarity transformation:
then the eigenvalues of T, which are also the eigenvalues of MAT, are computed
by a rational QR method [Reinsch_Bauer:1968].
Synopsis:
call select_eigval_cmp( mat(:n,:n) , eigval(:m) , small , failure , upper , d_e=d_e(:n,:2) ) call select_eigval_cmp( mat(:n,:n) , eigval(:m) , small , failure , d_e=d_e(:n,:2) ) call select_eigval_cmp( matp(:(n*(n+1)/2)) , eigval(:m) , small , failure , upper , d_e=d_e(:n,:2) ) call select_eigval_cmp( matp(:(n*(n+1)/2)) , eigval(:m) , small , failure , d_e=d_e(:n,:2) )
Examples:
-
select_eigval_cmp2()¶
Purpose:
select_eigval_cmp2() computes the largest or smallest eigenvalues of
a n-by-n real symmetric matrix MAT whose sum in
algebraic value (e.g. the sum of the absolute values) exceeds a given value.
MAT can be stored in packed form.
The matrix MAT is first transformed to symmetric tridiagonal form T
by an orthogonal similarity transformation:
then the eigenvalues of T, which are also the eigenvalues of MAT, are computed
by a rational QR method [Reinsch_Bauer:1968].
Synopsis:
call select_eigval_cmp2( mat(:n,:n) , eigval(:m) , small , val , failure , upper , d_e=d_e(:n,:2) ) call select_eigval_cmp2( mat(:n,:n) , eigval(:m) , small , val , failure , d_e=d_e(:n,:2) ) call select_eigval_cmp2( matp(:(n*(n+1)/2)) , eigval(:m) , small , val , failure , upper , d_e=d_e(:n,:2) ) call select_eigval_cmp2( matp(:(n*(n+1)/2)) , eigval(:m) , small , val , failure , d_e=d_e(:n,:2) )
Examples:
-
select_eigval_cmp3()¶
Purpose:
select_eigval_cmp3() computes the largest or smallest eigenvalues of
a n-by-n real symmetric matrix MAT, eventually stored in packed form.
The matrix MAT is first transformed to symmetric tridiagonal form T
by an orthogonal similarity transformation:
then the eigenvalues of T, which are also the eigenvalues of MAT, are computed
by a bisection method [Golub_VanLoan:1996].
The eigenvalues of T can be computed to high accuracy with the optional argument ABSTOL.
Synopsis:
call select_eigval_cmp3( mat(:n,:n) , neig , eigval(:n) , small , failure , upper , sort=sort , vector=vector , scaling=scaling , init=init , abstol=abstol , le=le , theta=theta , d_e=d_e(:n,:2) ) call select_eigval_cmp3( mat(:n,:n) , neig , eigval(:n) , small , failure , sort=sort , vector=vector , scaling=scaling , init=init , abstol=abstol , le=le , theta=theta , d_e=d_e(:n,:2) ) call select_eigval_cmp3( matp(:(n*(n+1)/2)) , neig , eigval(:n) , small , failure , upper , sort=sort , vector=vector , scaling=scaling , init=init , abstol=abstol , le=le , theta=theta , d_e=d_e(:n,:2) ) call select_eigval_cmp3( matp(:(n*(n+1)/2)) , neig , eigval(:n) , small , failure , sort=sort , vector=vector , scaling=scaling , init=init , abstol=abstol , le=le , theta=theta , d_e=d_e(:n,:2) )
Examples:
-
lae2()¶
Purpose:
lae2() computes the eigenvalues of a 2-by-2 symmetric matrix
On return, RT1 is the eigenvalue of larger absolute value, RT2 is the
eigenvalue of smaller absolute value.
This subroutine is from LAPACK.
Synopsis:
call lae2( a , b , c , rt1 , rt2 )
-
eigval_sort()¶
Given the eigenvalues D as output from eigval_cmp(),
eigval_cmp2(), eigval_cmp3(), symtrid_qri(), symtrid_qri2(), symtrid_qri3()
or other STATPACK routines which compute eigenvalues, eigval_sort() sorts
the eigenvalues D into ascending or descending order.
Synopsis:
call eigval_sort( sort , d(:m) )
Examples:
-
eigval_abs_sort()¶
Given the eigenvalues D as output from eigval_cmp(),
eigval_cmp2(), eigval_cmp3(), symtrid_qri(), symtrid_qri2(), symtrid_qri3()
or other STATPACK routines which compute eigenvalues, eigval_abs_sort() sorts
the eigenvalues D into ascending or descending order of absolute magnitude.
Synopsis:
call eigval_abs_sort( sort , d(:m) )
-
dflgen()¶
Purpose:
dflgen() computes deflation parameters (e.g. a chain of Givens rotations)
for a n-by-n symmetric unreduced tridiagonal matrix T and a given
eigenvalue LAMBDA of T.
On output, the arguments CS and SN contain, respectively, the vectors of the
cosines and sines coefficients of the chain of n-1 planar rotations that
deflates the real n-by-n symmetric tridiagonal matrix T corresponding to
the eigenvalue LAMBDA.
See [Malyshev:2000] for more details.
Synopsis:
call dflgen( d(:n) , e(:n-1) , lambda , cs(:n-1) , sn(:n-1) )
-
dflgen2()¶
Purpose:
dflgen2() computes and applies deflation parameters (e.g. a chain of Givens rotations)
for a n-by-n symmetric unreduced tridiagonal matrix T and a given
eigenvalue LAMBDA of T.
On output:
- the arguments D and E contain, respectively, the new main diagonal
and off-diagonal of the deflated symmetric tridiagonal matrix if
DEFLATE is set to
true. - the arguments CS and SN contain, respectively, the vectors of the
cosines and sines coefficients of the chain of
n-1planar rotations that deflates the realn-by-nsymmetric tridiagonal matrixTcorresponding to the eigenvalue LAMBDA.
See [Malyshev:2000] for more details.
Synopsis:
call dflgen2( d(:n) , e(:n-1) , lambda , cs(:n-1) , sn(:n-1) , deflate )
-
dflapp()¶
Purpose:
dflapp() deflates a n-by-n real symmetric tridiagonal matrix T by a chain
of planar rotations produced by dflgen().
On output, the arguments D and E contain, respectively, the new main diagonal
and off-diagonal of the deflated symmetric tridiagonal matrix, if DEFLATE is set
to true on output.
See [Malyshev:2000] for more details.
Synopsis:
call dflapp( d(:n) , e(:n-1) , cs(:n-1) , sn(:n-1) , deflate )
-
qrstep()¶
Purpose:
qrstep() performs one QR step with a given shift LAMBDA on a n-by-n real symmetric
unreduced tridiagonal matrix T.
On output, the arguments D and E contain, respectively, the new main diagonal
and off-diagonal of the deflated symmetric tridiagonal. The chain of n-1 planar
rotations produced during the QR step are saved in the arguments CS and SN.
See [Mastronardi_etal:2006] for more details.
Synopsis:
call qrstep( d(:n) , e(:n-1) , lambda , cs(:n-1) , sn(:n-1) , deflate )
-
prodgiv()¶
Purpose:
prodgiv() applies a chain of n-1 planar rotations produced by dflgen(), dflgen2() or qrstep()
to the vector argument X of length n. See [Mastronardi_etal:2006] for more details.
Synopsis:
call prodgiv( cs(:n-1) , sn(:n-1) , x(:n) )
-
prodgiv_eigvec()¶
Purpose:
prodgiv_eigvec() computes an approximate eigenvector of a n-by-n symmetric tridiagonal matrix from
a chain of n-1 planar rotations produced by dflgen(), dflgen2() or qrstep(). See
[Mastronardi_etal:2006] for more details.
Synopsis:
eigvec(:n) = prodgiv_eigvec( cs(:n-1) , sn(:n-1) )
-
symtrid_deflate()¶
Purpose:
symtrid_deflate() computes eigenvectors of a real symmetric tridiagonal
matrix T corresponding to specified eigenvalues, using sequential deflation techniques [Godunov_etal:1993]
[Malyshev:2000] [Mastronardi_etal:2006].
symtrid_deflate() may fail if some the eigenvalues specified in parameter EIGVAL are nearly identical or for clusters of small eigenvalues or for some zero-diagonal tridiagonal matrices.
symtrid_deflate() is a low-level routine used by the trid_deflate() driver routine. Its direct use as a method
for computing eigenvectors of a real symmetric tridiagonal matrix is not recommended.
Synopsis:
call symtrid_deflate( d(:n) , e(:n-1) , eigval , eigvec(:n) , failure , max_qr_steps=max_qr_steps ) call symtrid_deflate( d(:n) , e(:n-1) , eigval(:p) , eigvec(:n,:p) , failure(:p) , max_qr_steps=max_qr_steps )
-
trid_deflate()¶
Purpose:
trid_deflate() computes all or selected eigenvectors of a n-by-n real symmetric
tridiagonal T or full symmetric matrix MAT (eventually packed column-wise in a linear array MATP)
corresponding to specified eigenvalues, using deflation techniques [Godunov_etal:1993] [Malyshev:2000]
[Mastronardi_etal:2006].
If eigenvectors of a full symmetric matrix MAT are wanted, it is required that the original symmetric
matrix MAT has been reduced to symmetric tridiagonal form T by an orthogonal similarity transformation:
with a call to symtrid_cmp() with parameter STORE_Q set to true, before
calling trid_deflate().
The eigenvectors of T are computed using an efficient approach for the computation of (selected)
eigenvectors of a tridiagonal matrix corresponding to (selected) eigenvalues by combining
Fernando’s method for the computation of eigenvectors with deflation procedures by Givens
rotations [Fernando:1997] [Parlett_Dhillon:1997] [Malyshev:2000]. QR iterations are also used as
a back-up procedure if the deflation technique fails [Mastronardi_etal:2006].
If eigenvectors of a full symmetric matrix MAT are wanted, the computed eigenvectors of T are backed-transformed
to the eigenvectors of MAT using the packed representation of Q as computed by symtrid_cmp().
Both the computation of the eigenvectors of T and the back-transformation phase are parallelized with OpenMP [Walker:1988].
It is essential that eigenvalues given on entry of trid_deflate() are computed to
high (relative) accuracy. Subroutine symtrid_bisect() may be used for this purpose.
trid_deflate() may fail if some the eigenvalues specified in parameter EIGVAL are nearly identical for some pathological matrices or for clusters of small eigenvalues or for some zero-diagonal matrices.
The deflation algorithms used in trid_deflate() are competitive with the inverse iteration
procedure implemented in trid_inviter() subroutine.
Synopsis:
call trid_deflate( d(:n) , e(:n) , eigval(:p) , eigvec(:n,:p) , failure , max_qr_steps=max_qr_steps , ortho=ortho , inviter=inviter ) call trid_deflate( d(:n) , e(:n) , eigval(:p) , eigvec(:n,:p) , failure , mat(:n,:n) , max_qr_steps=max_qr_steps , ortho=ortho , inviter=inviter ) call trid_deflate( d(:n) , e(:n) , eigval(:p) , eigvec(:n,:p) , failure , matp(:(n*(n+1)/2)) , max_qr_steps=max_qr_steps , ortho=ortho , inviter=inviter )
Examples:
-
maxdiag_tinv_qr()¶
Purpose:
maxdiag_tinv_qr() computes the index of the element of maximum absolute value in the diagonal entries of
where T is a n-by-n symmetric tridiagonal matrix,
I is the identity matrix and lambda is a scalar.
The diagonal entries of ( T - lambda * I )-1 are computed by means of the QR
factorization of T - lambda * I.
For more details, see [Bini_etal:2005].
It is assumed that T is unreduced, but no check is done in the subroutine to verify
this assumption.
Synopsis:
maxdiag_tinv = maxdiag_tinv_qr( d(:n) , e(:n-1) , lambda )
-
maxdiag_tinv_ldu()¶
Purpose:
maxdiag_tinv_ldu() computes the index of the element of maximum absolute value in the diagonal entries of
where T is a n-by-n symmetric tridiagonal matrix,
I is the identity matrix and lambda is a scalar.
The diagonal entries of ( T - lambda * I )-1 are computed by means of LDU and UDL
factorization of T - lambda * I.
For more details, see [Fernando:1997].
It is assumed that T is unreduced, but no check is done in the subroutine to verify
this assumption.
Synopsis:
maxdiag_tinv = maxdiag_tinv_ldu( d(:n) , e(:n-1) , lambda )
-
trid_qr_cmp()¶
Purpose:
trid_qr_cmp() factorizes the symmetric matrix T - lambda * I, where
T is a n-by-n symmetric tridiagonal matrix,
I is the identity matrix and lambda is a scalar. as
where Q is an orthogonal matrix represented as the product of n-1 Givens
rotations and R is an upper triangular matrix with at most two non-zero
super-diagonal elements per column.
The parameter lambda is included in the routine so that trid_qr_cmp() may
be used to obtain eigenvectors of T by inverse iteration.
The subroutine also computes the index of the entry of maximum absolute value
in the diagonal of ( T - lambda * I )-1, which provides a good initial
approximation to start the inverse iteration process for computing the eigenvector
associated with the eigenvalue lambda.
For further details, see [Bini_etal:2005] [Fernando:1997] [Parlett_Dhillon:1997].
Synopsis:
call trid_qr_cmp( d(:n) , e(:n-1) , lambda , cs(:n-1) , sn(:n-1) , diag(:n) , sup1(:n) , sup2(:n) , maxdiag_tinv )
-
trid_qr_solve()¶
Purpose:
trid_qr_solve() may be used to solve for the vector x the system of equations
where T is a n-by-n symmetric tridiagonal matrix, I is the n-by-n
identity matrix, lambda and scale are scalars, following the factorization of
( T - lambda * I ) by trid_qr_cmp() or gk_qr_cmp(), as
where Q is an orthogonal matrix represented as the product of n-1 Givens
rotations and R is an upper triangular matrix with at most two non-zero
super-diagonal elements per column.
The matrix ( T - lambda * I ) is assumed to be ill-conditioned, and frequent rescalings
are carried out in order to avoid overflow. However, no test for singularity
or near-singularity is included in this routine. Such tests must be performed
before calling this routine. The scalar scale is not output by this routine
since this routine being intended for use in applications such as inverse iteration.
Synopsis:
call trid_qr_solve( cs(:n-1) , sn(:n-1) , diag(:n) , sup1(:n) , sup2(:n) , y(:n) )
-
trid_cmp()¶
Purpose:
trid_cmp() factorizes the symmetric matrix 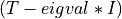 , where
, where
T is a n-by-n symmetric tridiagonal matrix, I is
the n-by-n identity matrix, eigval is a scalar, as
where P is a permutation matrix, L is a unit lower tridiagonal matrix
with at most one non-zero sub-diagonal elements per column and U is
an upper triangular matrix with at most two non-zero super-diagonal
elements per column.
The factorizations is obtained by Gaussian elimination with partial pivoting and implicit row scaling.
Several symmetric matrices 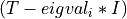 can be handled in a single call.
can be handled in a single call.
The parameter EIGVAL is included in the routine so that trid_cmp() may
be used to obtain eigenvectors of T by inverse iteration.
Synopsis:
call trid_cmp( d(:n) , e(:n) , eigval , sub(:n) , diag(:n) , sup1(:n) , sup2(:n) , perm(:n) , tol=tol ) call trid_cmp( d(:n) , e(:n) , eigval(:p) , sub(:p,:n) , diag(:p,:n) , sup1(:p,:n) , sup2(:p,:n) , perm(:p,:n) , tol=tol )
-
trid_cmp2()¶
Purpose:
trid_cmp2() factorizes the symmetric matrix 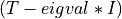 , where
, where
T is a n-by-n symmetric tridiagonal matrix, I is
the n-by-n identity matrix, eigval is a scalar, as
where P is a permutation matrix, L is a unit lower tridiagonal matrix
with at most one non-zero sub-diagonal elements per column and U is
an upper triangular matrix with at most two non-zero super-diagonal
elements per column.
The factorization is obtained by Gaussian elimination with partial pivoting and row interchanges.
Several symmetric matrices 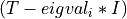 can be handled in a single call.
can be handled in a single call.
The parameter EIGVAL is included in the routine so that trid_cmp2() may
be used to obtain eigenvectors of T by inverse iteration.
trid_cmp2() is a simplified version of trid_cmp().
Synopsis:
call trid_cmp2( d(:n) , e(:n) , eigval , sub(:n) , diag(:n) , sup1(:n) , sup2(:n) , perm(:n) ) call trid_cmp2( d(:n) , e(:n) , eigval(:p) , sub(:p,:n) , diag(:p,:n) , sup1(:p,:n) , sup2(:p,:n) , perm(:p,:n) )
-
trid_solve()¶
Purpose:
trid_solve() may be used to solve for a vector x the system of equations
where T is a n-by-n symmetric tridiagonal matrix, I is the
n-by-n identity matrix, eigval and scale are scalars and y
is a vector, following the factorization of 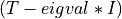 by
by trid_cmp() or trid_cmp2() as
where P is a permutation matrix, L is a unit lower tridiagonal matrix
with at most one non-zero sub-diagonal elements per column and U is
an upper triangular matrix with at most two non-zero super-diagonal
elements per column.
The matrix 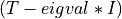 is assumed to be ill-conditioned, and frequent rescalings
are carried out in order to avoid overflow. However, no test for singularity
or near-singularity is included in this routine. Such tests must be performed
before calling this routine.
is assumed to be ill-conditioned, and frequent rescalings
are carried out in order to avoid overflow. However, no test for singularity
or near-singularity is included in this routine. Such tests must be performed
before calling this routine.
Several systems 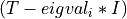 can be handled in a single call.
can be handled in a single call.
The scalar scale is not output by this routine since this routine being intended for
use in applications such as inverse iteration.
Synopsis:
call trid_solve( sub(:n) , diag(:n) , sup1(:n) , sup2(:n) , perm(:n) , y(:n) ) call trid_solve( sub(:p,:n) , diag(:p,:n) , sup1(:p,:n) , sup2(:p,:n) , perm(:p,:n) , y(:p,:n) )
-
trid_inviter()¶
Purpose:
trid_inviter() computes all or selected eigenvectors of a n-by-n real symmetric
tridiagonal T or full symmetric matrix MAT (eventually packed column-wise in a linear array MATP)
corresponding to specified eigenvalues, using inverse iteration and Fernando’s method [Golub_VanLoan:1996] [Ipsen:1997]
[Fernando:1997] [Bini_etal:2005].
If eigenvectors of a full symmetric matrix MAT are wanted, it is required that the original symmetric
matrix MAT has been reduced to symmetric tridiagonal form T by an orthogonal similarity transformation:
with a call to symtrid_cmp() with parameter STORE_Q set to true, before
calling trid_inviter().
The eigenvectors of T are computed using inverse iteration, combined with Fernando’s method, for all the eigenvalues at one step.
The eigenvectors are then orthogonalized by the Modified Gram-Schmidt algorithm if the eigenvalues are not well-separated
[Golub_VanLoan:1996] [Ipsen:1997].
If eigenvectors of a full symmetric matrix MAT are wanted, the computed eigenvectors of T are backed-transformed
to the eigenvectors of MAT using the packed representation of Q as computed by symtrid_cmp().
Both the computation of the eigenvectors of T and the back-transformation phase are parallelized with OpenMP [Walker:1988].
trid_inviter() may fail if some the eigenvalues specified in parameter EIGVAL are nearly identical for some pathological matrices.
Synopsis:
call trid_inviter( d(:n) , e(:n) , eigval , eigvec(:n) , failure , maxiter=maxiter , scaling=scaling , initvec=initvec ) call trid_inviter( d(:n) , e(:n) , eigval(:p) , eigvec(:n,:p) , failure , maxiter=maxiter , ortho=ortho , backward_sweep=backward_sweep , scaling=scaling , initvec=initvec ) call trid_inviter( d(:n) , e(:n) , eigval(:p) , eigvec(:n,:p) , failure , mat(:n,:n) , maxiter=maxiter , ortho=ortho , backward_sweep=backward_sweep , scaling=scaling , initvec=initvec ) call trid_inviter( d(:n) , e(:n) , eigval(:p) , eigvec(:n,:p) , failure , matp(:(n*(n+1)/2)) , maxiter=maxiter , ortho=ortho , backward_sweep=backward_sweep , scaling=scaling , initvec=initvec )
Examples:
-
gen_symtrid_mat()¶
Purpose:
gen_symtrid_mat() generates different types of symmetric tridiagonal matrices with known eigenvalues or specific numerical properties such as clustered eigenvalues and so on for testing purposes of eigensolvers.
Optionally, the eigenvalues of the selected symmetric tridiagonal matrix can be computed analytically, if possible, or by a bisection algorithm with high absolute and relative accuracies.
Synopsis:
call gen_symtrid_mat( type , d(:n) , e(:n) , failure=failure , known_eigval=known_eigval , eigval=eigval , sort=sort , val1=val1 , val2=val2 , l0=l0 , glu0=glu0 )