MODULE Random

Module Random exports subroutines and functions for random number and array generation and related procedures.

Some parts of this module are adapted from [Hennecke:1995]. Note also that the successful compilation of the Random module (e.g. the file Module_Random.F90 in the $STATPACKDIR/sources directory) on your system may require the use of some cpp macros. See the section Preprocessor cpp macros for more details.

This module may be used to replace the Fortran 90 intrinsic routines random_number() and random_seed() by several implementations of the Marsaglia’s KISS (e.g. Keep It Simple Stupid), L’Ecuyer’s LFSR113, Mersenne Twister’s MT19937 AND MEMT19937-II uniform random generators.

The Marsaglia’s KISS (Keep It Simple Stupid) random number generator combines:

1. The congruential generator with a period of 2³²;
2. A 3-shift shift-register generator with a period of 2³² - 1;
3. Two 16-bit multiply-with-carry generators with a period of 597273182964842497 > 2⁵⁹.

The overall period of this KISS random number generator exceeds 2¹²³. More details on this Marsaglia’s KISS random number generator are available in the references [Marsaglia:1999] and [Marsaglia:2005]. This generator is also the one supplied by the intrinsic subroutine random_number() as implemented in the GNU gfortran compiler.

The module also includes a “fast” version of the KISS random number generator, which uses only add, shift, exclusive-or and ‘and’ operations to produces exactly the same 32-bit integer output, which C views as unsigned and Fortran views as signed integers. This KISS version avoids multiplication and is probably faster. More details are available in [Marsaglia:2007].

The LFSR113 random number generator is described in [LEcuyer:1999]. This random number generator has a period length of about 2¹¹³

The MT19937 Mersenne Twister random number generator is described in [Matsumoto_Nishimura:1998]. This random number generator has a period length of about 2¹⁹⁹³⁷ - 1, and 623-dimensional equidistribution property is assured. This random number generator is also the one supplied by the intrinsic subroutine random_number() as implemented by the NAG nagfor compiler.

The MEMT19937-II Mersenne Twister random number generator is described in [Harase:2014]. This random number generator has also a period length of about 2¹⁹⁹³⁷ - 1, and a new set of parameters is introduced in the tempering phase of MT19937, which gives a maximally equidistributed Mersenne Twister random number generator.

For all the random number generators described above, extended precision versions are also available to generate full precision random real numbers of kind stnd (up to 63-bit precision) using the method described in [Doornik:2007].

The choice between these 10 different uniform random generators can be done with a call to the subroutine random_seed_() by specifying the optional ALG argument (see below).

The FORTRAN versions of these random number generators as implemented here require that 32-bits integer type is available on your computer and that 32-bits integers are represented in base 2 with two’s complement notation.

However, the LFSR113, MT19937 and MEMT19937-II Mersenne Twister random number generators will also work if only 64-bits integer type is available on your system, but in that case you must specify the cpp macro _RANDOM_NOINT32 at compilation of the STATPACK library. See the section Preprocessor cpp macros for more details. The other random number generators will not work properly with 64-bits integer type so they cannot be used on such system.

The KISS random number generators also assumed that integer overflows do not cause crashes. These assumptions are checked before using these random number generators. On the other hand, the LFSR113, MT19937 and MEMT19937-II random number generators do not use integer arithmetic and are free of such assumptions.

These 10 different uniform random generators are implemented by the routines random_number_() and random_seed_(), described below, and which also follow the standard Fortran 90 interfaces defined by the intrinsic procedures random_number() and random_seed() [Fortran]. The only exception is the addition of the optional argument ALG in the random_seed_() subroutine, which allows the user to select the random generator he wants to use subsequently in his Fortran program.

The random_seed_() subroutine can be used to seed the different STATPACK random generators as defined in the Fortran standard [Fortran]. Note, however, that both the different versions of the MT19937 and MEMT19937-II random number generators have a very large state (630 32-bit integers), and therefore it is strongly recommended that the random_seed_() routine only be used with a PUT argument that is the value returned by a previous call with a GET argument; i.e., only to repeat a previous sequence for these generators. This is because if a user-specified seed has low entropy (likely since there are 630 values to be supplied), it is highly likely to set these generators to an apparently-low-entropy part of their sequence.

Moreover, as the seed is used as a random bit-stream, it is expected to have approximately half of its bits nonzero. Thus, providing many small integer values will likely result in a low-entropy part of the MT19937 and MEMT19937-II sequences being reached (this is also true for the other STATPACK random generators).

If you do want to provide your own seed (and thus entropy), for the MT19937 and MEMT19937-II random number generators, it is better to use the init_mt19937() and init_memt19937() subroutines (described below), which allow you to use any size for their integer seed vector argument, but limit the risk of reaching a low-entropy part of the MT19937 and MEMT19937-II sequences.

In order to use routines random_number_() and random_seed_() provided by module Random instead of the intrinsic Fortran 90 procedures random_number() and random_seed() in your Fortran program, include an appropriate use Random (or use Statpack) statement, like:

use Random, only: random_number=>random_number_, random_seed=>random_seed_

In addition to these different uniform random real generators, this module also provides:

• subroutines and functions for random (signed and unsigned) integer generation;
• Gaussian random generators [Thomas_etal:2007];
• shuffling and sampling routines [Noreen:1989];
• subroutines for generating pseudo-random orthogonal matrices following the Haar distribution over the group of orthogonal matrices [Stewart:1980];
• subroutines for generating pseudo-random symmetric matrices with a prescribed spectrum;
• subroutines for generating pseudo-random matrices with a prescribed singular value distribution.

The Gaussian random generators provided in this module use the classical Box-Muller method or the Cumulative Density Function (CDF) inversion method to generate Gaussian random real numbers of kind stnd or extd [Thomas_etal:2007].

Random generators for other probability distribution functions are not provided in this version of STATPACK, but can be easily constructed with the help of the inverse distribution functions included in the Prob_procedures module.

In order to use one of the routines provided by the Random module, you must include an appropriate use Random or use Statpack statement in your Fortran program, like:

use Random, only: rand_number

or :

use Statpack, only: rand_number

Here is the list of the public routines exported by module Random:

random_seed_()

Purpose:

This subroutine provides an user interface for seeding the random number routines in module Random.

Syntax is like random_seed() intrinsic subroutine and a call to random_seed_() without arguments initiates a non-repeatable reset of the seeds used by the random number subroutines and functions in module Random.

As for random_seed() intrinsic subroutine, no more than one argument may be specified in a call to random_seed_().

Note that the size of the seed array varies according to the selected random generator (e.g. with the value of the optional ALG argument).

Synopsis:

call random_seed_( alg=alg , size=size , put=put , get=get )

Examples:

ex1_random_svd.F90

ex1_random_eig.F90

ex1_random_eig_pos.F90

init_mt19937()

Purpose:

User interface subroutine for initializing the state of the MT19937 Random Number Generator (RNG) with a scalar or vector integer seed of kind i4b directly, without using the subroutine random_seed_() and its interface.

Synopsis:

call init_mt19937( seed    )
call init_mt19937( seed(:) )

init_memt19937()

Purpose:

User interface subroutine for initializing the state of the MEMT19937-II Random Number Generator (RNG) with a scalar or vector integer seed of kind i4b directly, without using the subroutine random_seed_() and its interface.

Synopsis:

call init_memt19937( seed    )
call init_memt19937( seed(:) )

rand_number()

Purpose:

This function returns an uniformly distributed random number between 0 and 1, exclusive of the two endpoints 0 and 1.

However, if the cpp macro _RANDOM_WITH0 is used for the compilation of the STATPACK library, this function may return the zero value.

Synopsis:

harvest = rand_number( ) ! harvest is a real number of kind stnd

random_number_()

Purpose:

This generic subroutine returns an uniformly distributed random array (or number) between 0 and 1, exclusive of the two endpoints 0 and 1.

However, if the cpp macro _RANDOM_WITH0 is used for the compilation of the STATPACK library, this subroutine may return the zero value.

Synopsis:

call random_number_( harvest )                ! harvest is an uniform random real number of kind stnd between 0 and 1
call random_number_( harvest(:) )             !
call random_number_( harvest(:,:) )           !
call random_number_( harvest(:,:,:) )         !
call random_number_( harvest(:,:,:,:) )       ! harvest is an uniform random real array of kind stnd between 0 and 1
call random_number_( harvest(:,:,:,:,:) )     !
call random_number_( harvest(:,:,:,:,:,:) )   !
call random_number_( harvest(:,:,:,:,:,:,:) ) !

Examples:

ex1_random_number_.F90

rand_integer32()

Purpose:

This function returns a random integer in the interval (-2147483648 , 2147483647) inclusive of the two endpoints.

The returned integer is equivalent to a signed 32-bit integer.

Synopsis:

harvest = rand_integer32( ) ! harvest is a signed 32-bit integer of kind i4b

random_integer32_()

Purpose:

This generic subroutine returns an array (or number) of random integers in the interval (-2147483648 , 2147483647) inclusive of the two endpoints.

The returned integers are equivalent to signed 32-bit integers.

Synopsis:

call random_integer32_( harvest )                ! harvest is an uniform random signed 32-bit integer of kind i4b
call random_integer32_( harvest(:) )             !
call random_integer32_( harvest(:,:) )           !
call random_integer32_( harvest(:,:,:) )         !
call random_integer32_( harvest(:,:,:,:) )       ! harvest is an uniform random signed 32-bit integer array of kind i4b
call random_integer32_( harvest(:,:,:,:,:) )     !
call random_integer32_( harvest(:,:,:,:,:,:) )   !
call random_integer32_( harvest(:,:,:,:,:,:,:) ) !

rand_integer31()

Purpose:

This function returns a random integer in the interval (0 , 2147483647) inclusive of the two endpoints.

The returned integer is equivalent to an unsigned 31-bit integer.

Synopsis:

harvest = rand_integer31( ) ! harvest is an unsigned (positive) 31-bit integer of kind i4b

random_integer31_()

Purpose:

This generic subroutine returns an array (or number) of random integers in the interval (0 , 2147483647) inclusive of the two endpoints.

The returned integers are equivalent to unsigned 31-bit integers.

Synopsis:

call random_integer31_( harvest )                ! harvest is an uniform random unsigned 31-bit integer of kind i4b
call random_integer31_( harvest(:) )             !
call random_integer31_( harvest(:,:) )           !
call random_integer31_( harvest(:,:,:) )         !
call random_integer31_( harvest(:,:,:,:) )       ! harvest is an uniform random unsigned 31-bit integer array of kind i4b
call random_integer31_( harvest(:,:,:,:,:) )     !
call random_integer31_( harvest(:,:,:,:,:,:) )   !
call random_integer31_( harvest(:,:,:,:,:,:,:) ) !

normal_rand_number()

Purpose:

This function returns a Gaussian distributed random real number of kind stnd.

This function uses a Cumulative Density Function (CDF) inversion method to generate a Gaussian random real number of kind stnd.

Synopsis:

harvest = normal_rand_number( ) ! harvest is a real number of kind stnd

normal_random_number_()

Purpose:

This generic subroutine returns a random number/array HARVEST of kind stnd following the standard normal (Gaussian) distribution.

This subroutines uses a Cumulative Density Function (CDF) inversion method to generate Gaussian random numbers of kind stnd.

Synopsis:

call normal_random_number_( harvest )       ! harvest is a Gaussian distributed random real number of kind stnd
call normal_random_number_( harvest(:) )    ! harvest is a Gaussian distributed random real vector of kind stnd
call normal_random_number_( harvest(:,:) )  ! harvest is a Gaussian distributed random real matrix of kind stnd

Examples:

ex1_normal_random_number_.F90

normal_rand_number2()

Purpose:

This function returns a Gaussian distributed random real number of kind extd.

This function uses a Cumulative Density Function (CDF) inversion method to generate a Gaussian random real number of kind extd and is more accurate than function normal_rand_number() even if kinds extd and stnd are equivalent.

Synopsis:

harvest = normal_rand_number2( ) ! harvest is a real number of kind extd

normal_random_number2_()

Purpose:

This generic subroutine returns a random number/array HARVEST of kind extd following the standard normal (Gaussian) distribution.

This subroutines uses a Cumulative Density Function (CDF) inversion method to generate Gaussian random numbers of kind extd and is more accurate than subroutine normal_random_number() even if kinds extd and stnd are equivalent.

Synopsis:

call normal_random_number2_( harvest )       ! harvest is a Gaussian distributed random real number of kind extd
call normal_random_number2_( harvest(:) )    ! harvest is a Gaussian distributed random real vector of kind extd
call normal_random_number2_( harvest(:,:) )  ! harvest is a Gaussian distributed random real matrix of kind extd

Examples:

ex1_normal_random_number2_.F90

normal_rand_number3()

Purpose:

This function returns a Gaussian distributed random real number of kind stnd.

This function uses the classical Box-Muller method to generate a Gaussian random real number of kind stnd.

Synopsis:

harvest = normal_rand_number3( ) ! harvest is a real number of kind stnd

normal_random_number3_()

Purpose:

This generic subroutine returns a random number/array HARVEST of kind stnd following the standard normal (Gaussian) distribution.

This subroutine uses the classical Box-Muller method to generate Gaussian random real numbers of kind stnd.

Synopsis:

call normal_random_number3_( harvest )       ! harvest is a Gaussian distributed random real number of kind stnd
call normal_random_number3_( harvest(:) )    ! harvest is a Gaussian distributed random real vector of kind stnd
call normal_random_number3_( harvest(:,:) )  ! harvest is a Gaussian distributed random real matrix of kind stnd

Examples:

ex1_normal_random_number3_.F90

ex1_random_svd.F90

ex1_random_eig.F90

ex1_random_eig_pos.F90

random_qr_cmp()

Purpose:

This subroutine generates the first k columns of a pseudo-random QR factorization (in factored form) of a hypothetical real n-by-n matrix MAT, whose elements follow independently the standard normal distribution:

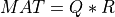
where Q is a pseudo-random orthogonal matrix following the Haar distribution from the group of orthogonal matrices and R is upper triangular.

The upper-diagonal elements of R follow the standard normal distribution and the squares of the diagonal elements of R, R(i,i)², follow a chi-squared distribution with n-i+1 degrees of freedom.

This subroutine uses a fast method based on Householder transformations for generating the first k columns of a n-by-n pseudo-random orthogonal matrices Q distributed according to the Haar measure over the orthogonal group of order n, in a factored form [Stewart:1980].

Synopsis:

call random_qr_cmp( mat(:n,:k) , diagr(:k) , beta(:k) , fillr=fillr , initseed=initseed )

ortho_gen_random_qr()

Purpose:

This subroutine generates a n-by-n real pseudo-random orthogonal matrix following the Haar distribution, which is defined as the product of n elementary Householder reflectors of order n and of a n-by-n diagonal matrix with diagonal elements equal to sign( one, DIAGR) [Stewart:1980]:

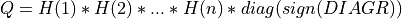
as returned by subroutine random_qr_cmp().

Synopsis:

call ortho_gen_random_qr( mat(:n,:k) , diagr(:k) , beta(:k) )

gen_random_sym_mat()

Purpose:

This subroutine generates a pseudo-random n-by-n real symmetric matrix with prescribed eigenvalues.

Optionally, the corresponding eigenvectors of the generated pseudo-random n-by-n real symmetric matrix can be computed if required.

Synopsis:

call gen_random_sym_mat( eigval(:k) , mat(:n,:n) , eigvec=eigvec(:n,:k) , initseed=initseed )

Examples:

ex1_random_eig.F90

ex1_random_eig_pos.F90

gen_random_mat()

Purpose:

This subroutine generates a pseudo-random m-by-n real matrix with prescribed singular values.

Optionally, the corresponding singular vectors of the generated pseudo-random m-by-n real matrix can be computed if required.

Synopsis:

call gen_random_mat( eigval(:k) , mat(:m,:n) , leftvec=leftvec(:m,:k) , rightvec=rightvec(:n,:k) , initseed=initseed )

Examples:

ex1_random_svd.F90

simple_shuffle()

Purpose:

This generic subroutine shuffles all the elements of the vector VEC.

Synopsis:

call simple_shuffle( vec(:) ) ! vec is a real     vector of kind stnd
call simple_shuffle( vec(:) ) ! vec is a complex  vector of kind stnd
call simple_shuffle( vec(:) ) ! vec is an integer vector of kind i4b

drawsample()

Purpose:

This subroutine may be used to draw a sample, without replacement of size NSAMPLE from a population of size SIZE(POP). On output, the integer vector POP(1:NSAMPLE) indicates which observations are included in the sample.

The integer vector POP must be dimensioned at least as large as NSAMPLE in the calling program.

Synopsis:

call drawsample( nsample , pop(:) ) ! pop is an integer vector of kind i4b

Exemples:

ex1_drawsample.F90

ex2_drawsample.F90

drawbootsample()

Purpose:

This subroutine may be used to draw a bootstrap random sample of size SIZE(SAMPLE) from a finite population of size NPOP. On output, the integer vector SAMPLE indicates which observations are included in the bootstrap sample.

The sampling is done with replacement, meaning that the sample may contain duplicate observations.

Synopsis:

call drawbootsample( npop , sample(:) ) ! sample is an integer vector of kind i4b