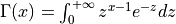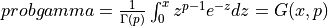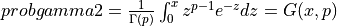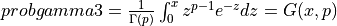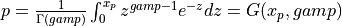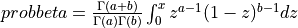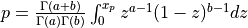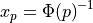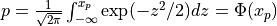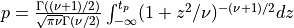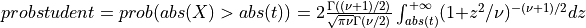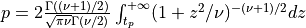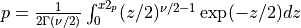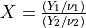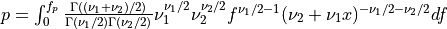MODULE Prob_Procedures¶
Module Prob_Procedures exports subroutines and functions for probability distribution functions and their inverses.
A very good introduction to probability distribution functions and algorithms used in this module can be found in [Walck:2007].
In order to use one of these routines, you must include an appropriate use Prob_Procedures or use Statpack statement
in your Fortran program, like:
use Prob_Procedures, only: lngamma
or:
use Statpack, only: lngamma
Here is the list of the public routines exported by module Prob_Procedures:
-
lngamma()¶
Purpose:
lngamma() evaluates the logarithm of the gamma function 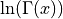 for a strictly positive real argument X.
for a strictly positive real argument X.
Argument X can be a scalar, a vector or a matrix.
The gamma function is defined as,
for x > 0.
This function uses a Lanczos-type approximation to 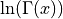 for
for x > 0 [Lanczos:1964].
Its accuracy is about 14 significant digits except for small regions in the vicinity of 1 and 2.
The function is parallelized when X is a vector or matrix argument, if OPENMP is used.
Synopsis:
lngam = lngamma( x ) lngam(:n) = lngamma( x(:n) ) lngam(:n,:m) = lngamma( x(:n,:m) )
-
probgamma()¶
Purpose:
probgamma() evaluates the gamma probability distribution function (e.g. the Incomplete Gamma Integral)
for a positive real scalar (vector or matrix) argument X and a strictly positive value (vector or matrix)
argument GAMP of the parameter p of the Gamma distribution.
probgamma() computes the probability that a random variable having a Gamma distribution
with parameter p (given on input by GAMP) will be less than or equal to x:
For large GAMP (e.g. GAMP > 1000), this function uses a normal approximation, based
on the Wilson-Hilferty transformation, see [Abramowitz_Stegun:1970], Formula 26.4.14, for more details.
Otherwise, a Pearson’s series expansion is used for evaluating the integral, see [Abramowitz_Stegun:1970], Formula 6.5.29. The integrating process is terminated when both the absolute and relative contributions to the integral is not greater than the value of the optional argument ACU. The default value for ACU gives the maximum precision of this function.
The time taken by this function thus depends in the precision requested through the ACU argument, and also varies slightly with the input arguments X and GAMP.
The function is parallelized when X is a vector or matrix argument, if OPENMP is used.
This function is more accurate than probgamma3(), but it may be slower.
Fore more details and algorithms, see [Lau:1980] and [Shea:1988].
Synopsis:
p = probgamma( x , gamp , acu=acu , maxiter=maxiter , failure=failure ) p(:n) = probgamma( x(:n) , gamp , acu=acu , maxiter=maxiter , failure=failure ) p(:n,:m) = probgamma( x(:n,:m) , gamp , acu=acu , maxiter=maxiter , failure=failure ) p(:n) = probgamma( x(:n) , gamp(:n) , acu=acu , maxiter=maxiter , failure=failure ) p(:n,:m) = probgamma( x(:n,:m) , gamp(:n,:m) , acu=acu , maxiter=maxiter , failure=failure )
-
probgamma2()¶
Purpose:
probgamma2() evaluates the gamma probability distribution function (e.g. the Incomplete Gamma Integral)
for a positive real scalar (vector or matrix) argument X and a strictly positive value (vector or matrix)
argument GAMP of the parameter p of the Gamma distribution.
probgamma2() computes the probability that a random variable having a Gamma distribution
with parameter p (given on input by GAMP) will be less than or equal to x:
For large GAMP (e.g. GAMP > 1000), this function uses a normal approximation, based
on the Wilson-Hilferty transformation, see [Abramowitz_Stegun:1970], Formula 26.4.14, for more details.
For X <= 1 or X < GAMP, a Pearson’s series expansion is used, see [Abramowitz_Stegun:1970],
Formula 6.5.29, p.262. For other values of X, a continued fraction expansion is
used since this expansion tends to converge more quickly than Pearson’s series
expansion (used in probgamma()), see [Abramowitz_Stegun:1970], Formula 6.5.31, p.263.
In both cases, the integrating process is terminated when both the absolute and relative contributions to the integral is not greater than the value of ACU. The default value for ACU gives the maximum precision of this function.
The function is parallelized when X is a vector or matrix argument, if OPENMP is used.
The time taken by this function thus depends in the precision requested through the ACU argument, and also varies slightly with the input arguments X and GAMP.
This function is more accurate than probgamma3(), but it is slower.
Fore more details and algorithms, see [Lau:1980] and [Shea:1988].
Synopsis:
p = probgamma2( x , gamp , acu=acu , maxiter=maxiter , failure=failure ) p(:n) = probgamma2( x(:n) , gamp , acu=acu , maxiter=maxiter , failure=failure ) p(:n,:m) = probgamma2( x(:n,:m) , gamp , acu=acu , maxiter=maxiter , failure=failure ) p(:n) = probgamma2( x(:n) , gamp(:n) , acu=acu , maxiter=maxiter , failure=failure ) p(:n,:m) = probgamma2( x(:n,:m) , gamp(:n,:m) , acu=acu , maxiter=maxiter , failure=failure )
-
probgamma3()¶
Purpose:
probgamma3() evaluates the gamma probability distribution function (e.g. the Incomplete Gamma Integral)
for a positive real scalar (vector or matrix) argument X and a strictly positive value (vector or matrix)
argument GAMP of the parameter p of the Gamma distribution.
probgamma3() computes the probability that a random variable having a Gamma distribution
with parameter p (given on input by GAMP) will be less than or equal to x:
For large GAMP (e.g. GAMP > 1000), this function uses a normal approximation, based
on the Wilson-Hilferty transformation, see [Abramowitz_Stegun:1970], Formula 26.4.14, for more details.
For X<=max(GAMP/2,13), a Pearson’s series expansion is used, see [Abramowitz_Stegun:1970], Formula 6.5.29, p.262. For larger values of X, an alternate Pearson’s asymptotic series expansion is used since this expansion tends to converge more quickly [Shea:1988], see [Abramowitz_Stegun:1970], Formula 6.5.32, p.263.
In both cases, the integrating process is terminated when both the absolute and relative contributions to the integral is not greater than the value of ACU. The default value for ACU gives the maximum precision of this function.
The time taken by this function thus depends in the precision requested through the ACU argument, and also varies slightly with the input arguments X and GAMP.
The function is parallelized when X is a vector or matrix argument, if OPENMP is used.
probgamma3() is faster, but less accurate than probgamma() or probgamma2() since,
for large values of X, the alternate Pearson’s series expansion is only asymptotic.
Fore more details and algorithms, see [Lau:1980] and [Shea:1988].
Synopsis:
p = probgamma3( x , gamp , acu=acu , maxiter=maxiter , failure=failure ) p(:n) = probgamma3( x(:n) , gamp , acu=acu , maxiter=maxiter , failure=failure ) p(:n,:m) = probgamma3( x(:n,:m) , gamp , acu=acu , maxiter=maxiter , failure=failure ) p(:n) = probgamma3( x(:n) , gamp(:n) , acu=acu , maxiter=maxiter , failure=failure ) p(:n,:m) = probgamma3( x(:n,:m) , gamp(:n,:m) , acu=acu , maxiter=maxiter , failure=failure )
-
pinvgamma()¶
Purpose:
pinvgamma() evaluates the inverse gamma probability distribution function.
For given arguments P (0 <= P <= 1) and GAMP (GAMP > 0), PINVGAMMA returns
the value 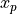 such that P is the probability that a random variable distributed as a gamma distribution
with parameter
such that P is the probability that a random variable distributed as a gamma distribution
with parameter gamp (given on input by GAMP) is less than or equal to 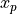 .
.
In other words, pinvgamma() returns the gamma deviate 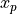 corresponding to a given lower tail area of
corresponding to a given lower tail area of p of the gamma distribution with parameter gamp:
This function actually uses the pinvq2() function and is adapted from [Best_Roberts:1975] [Shea:1988] [Shea:1991].
Synopsis:
x = pinvgamma( p , gamp , acu=acu , maxiter=maxiter )
-
probbeta()¶
Purpose:
probbeta() evaluates the beta probability distribution function (e.g the Incomplete Beta Function).
For given arguments X ( 0 <= X <= 1 ), A ( A > 0 ), B ( B > 0 ),
probbeta() returns the probability that a random variable from a beta distribution having parameters
a and b will be less than or equal to x,
Argument X can be a scalar, a vector or a matrix.
The function is parallelized when X is a vector or matrix argument, if OPENMP is used.
This function is adapted from [Majumder_Bhattacharjee:1973] [Cran_etal:1977].
Synopsis:
p = probbeta( x , a , b , beta=beta , acu=acu , maxiter=maxiter , failure=failure ) p(:n) = probbeta( x(:n) , a , b , beta=beta , acu=acu , maxiter=maxiter , failure=failure ) p(:n,:m) = probbeta( x(:n,:m) , a , b , beta=beta , acu=acu , maxiter=maxiter , failure=failure )
Examples:
-
pinvbeta()¶
Purpose:
pinvbeta() evaluates the inverse beta probability distribution function (e.g. the Incomplete Beta Function).
For given arguments P ( 0 <= P <= 1 ), A ( A > 0.1 ), B ( B > 0.1 ), pinvbeta()
returns the value 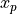 such that
such that p is the probability that a random variable distributed as 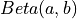 (e.g. the standard probability Beta distribution) is less than or equal to
(e.g. the standard probability Beta distribution) is less than or equal to 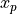 .
.
In other words, pinvbeta() returns the beta deviate 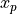 corresponding to a given lower tail area of
corresponding to a given lower tail area of p of
the beta distribution with parameters a and a (given on input by the arguments A and B, respectively):
This function is not very accurate for small values of A and/or B (e.g. less than 0.5).
For more details and algorithms, see [Majumder_Bhattacharjee:1973] [Cran_etal:1977] [Berry_etal:1990] [Berry_etal:1991].
Synopsis:
x = pinvbeta( p , a , b , beta=beta , acu=acu , maxiter=maxiter )
-
probn()¶
Purpose:
probn() evaluates the standard normal (Gaussian) distribution function from X to infinity
if UPPER is true or from minus infinity to X if UPPER is false.
In other words:
if UPPER =
true: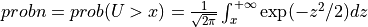
if UPPER =
false: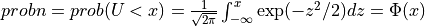
for U following a standard normal distribution: 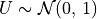 .
.
It is accurate at least to 10 places (for double-precision data).
Real argument X is of kind stnd and the result of probn() is also returned as real data of kind stnd.
Argument X can be a scalar, a vector or a matrix.
The function is parallelized when X is a vector or matrix argument, if OPENMP is used.
This function is adapted from [Hill:1973].
Synopsis:
p = probn( x , upper ) p(:n) = probn( x(:n) , upper ) p(:n,:m) = probn( x(:n,:m) , upper )
Examples:
-
pinvn()¶
Purpose:
pinvn() evaluates the inverse of the standard normal (Gaussian) distribution function for the argument P,
with 0 < P < 1,
where 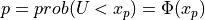 for
for U following a standard normal distribution: 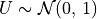 .
.
In other words, pinvn() returns the normal deviate 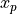 corresponding to a given lower tail area of
corresponding to a given lower tail area of p of the standard
normal distribution:
The inverse Gaussian Cumulative Distribution Function (CDF) is approximated to high precision using rational approximations (polynomials with degree 2 and 3) by the subroutine PPND7 given in [Wichura:1988].
This function is accurate to about seven decimal figures for 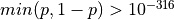 .
.
Real argument P is of kind stnd and the result of pinvn() is also returned as real data of kind stnd.
Argument P can be a scalar, a vector or a matrix.
The function is parallelized when P is a vector or matrix argument, if OPENMP is used.
Synopsis:
x = pinvn( p ) x(:n) = pinvn( p(:n) ) x(:n,:m) = pinvn( p(:n,:m) )
Examples:
-
probn2()¶
Purpose:
probn2() evaluates the standard normal (Gaussian) distribution function from X to infinity
if UPPER is true or from minus infinity to X if UPPER is false.
In other words:
if UPPER =
true: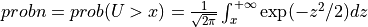
if UPPER =
false: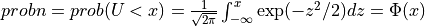
for U following a standard normal distribution: 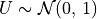 .
.
Real argument X is of kind extd and the result of probn2() is also returned as real data of kind extd.
Argument X can be a scalar, a vector or a matrix.
This function is parallelized when X is a vector or matrix argument if OPENMP is used.
probn2() is based upon algorithm 5666 for the error function from [Hart:1978] and
is more accurate than probn().
Synopsis:
p = probn2( x , upper ) p(:n) = probn2( x(:n) , upper ) p(:n,:m) = probn2( x(:n,:m) , upper )
Examples:
-
pinvn2()¶
Purpose:
pinvn2() evaluates the inverse of the standard normal (Gaussian) distribution function for the argument P,
with 0 < P < 1,
where 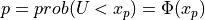 for
for U following a standard normal distribution: 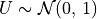 .
.
In other words, pinvn2() returns the normal deviate 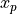 corresponding to a given lower tail area of
corresponding to a given lower tail area of p of the standard
normal distribution:
The inverse Gaussian Cumulative Distribution Function (CDF) is approximated to high precision using rational approximations (polynomials with degree 7) by the subroutine PPND16 given in [Wichura:1988].
This function is accurate to about seven decimal figures for 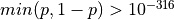 .
.
Real argument P is of kind extd and the result of pinvn2() is also returned as real data of kind extd.
Argument P can be a scalar, a vector or a matrix.
The function is parallelized when P is a vector or matrix argument, if OPENMP is used.
Synopsis:
x = pinvn2( p ) x(:n) = pinvn2( p(:n) ) x(:n,:m) = pinvn2( p(:n,:m) )
Examples:
-
probt()¶
Purpose:
probt() evaluates the Student’s t-distribution function with NDF degrees of freedom from T (T can be a scalar,
a vector or a matrix) to infinity if UPPER is true or from minus infinity to T if UPPER is false.
In other words,
if UPPER =
true: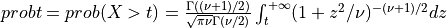
if UPPER =
false: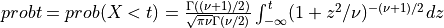
for X following a Student’s t-distribution with 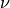 degrees of freedom (given on input by the argument NDF):
degrees of freedom (given on input by the argument NDF): 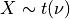 .
.
Argument T is of kind stnd and can be a scalar, a vector or a matrix.
This function is parallelized when T is a vector or matrix argument if OPENMP is used.
This function is adapted from [Cooper:1968] [Hill:1970].
Synopsis:
p = probt( t , ndf , upper, ndf_max=ndf_max ) p(:n) = probt( t(:n) , ndf , upper, ndf_max=ndf_max ) p(:n,:m) = probt( t(:n,:m) , ndf , upper, ndf_max=ndf_max ) p(:n) = probt( t(:n) , ndf(:n) , upper, ndf_max=ndf_max ) p(:n,:m) = probt( t(:n,:m) , ndf(:n,:m) , upper, ndf_max=ndf_max )
Examples:
-
pinvt()¶
Purpose:
pinvt() evaluates the inverse of the Student’s t distribution function with NDF degrees of freedom for the argument P,
with 0 < P < 1 (P can be a scalar, a vector or a matrix).
In other words, pinvt() returns the quantile 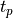 of Student’s t-distribution with
of Student’s t-distribution with 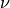 degrees of
freedom (given in the argument NDF) corresponding to a given lower tail area of
degrees of
freedom (given in the argument NDF) corresponding to a given lower tail area of p:
Argument P is of kind stnd and can be a scalar, a vector or a matrix.
This function is parallelized when P is a vector or matrix argument if OPENMP is used.
This function is adapted from [Hill:1970b].
Synopsis:
t = pinvt( p , ndf ) t(:n) = pinvt( p(:n) , ndf ) t(:n,:m) = pinvt( p(:n,:m) , ndf ) t(:n) = pinvt( p(:n) , ndf(:n) ) t(:n,:m) = pinvt( p(:n,:m) , ndf(:n,:m) )
Examples:
-
probstudent()¶
Purpose:
probstudent() evaluates the two-tailed probability of Student’s t with DF degrees of freedom.
probstudent() computes the probability that a random variable following the Student’s t
distribution with 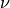 degrees of freedom (given in the argument DF) will exceed
degrees of freedom (given in the argument DF) will exceed
abs(t) (T can be a scalar, a vector or a matrix) in absolute value:
for X following a Student’s t-distribution with 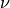 degrees of freedom:
degrees of freedom: 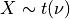 .
.
This function is not very accurate for very small degrees of freedom (e.g. number of
degrees of freedom less than 5).
Argument T is of kind stnd and can be a scalar, a vector or a matrix.
This function is parallelized when T is a vector or matrix argument if OPENMP is used.
This function is adapted from [Hill:1970].
Synopsis:
p = probstudent( t , df ) p(:n) = probstudent( t(:n) , df ) p(:n,:m) = probstudent( t(:n,:m) , df ) p(:n) = probstudent( t(:n) , df(:n) ) p(:n,:m) = probstudent( t(:n,:m) , df(:n,:m) )
Examples:
-
pinvstudent()¶
Purpose:
pinvstudent() evaluates the inverse of a modification of Student’s t probability distribution function.
pinvstudent() calculates the two-tail quantile of Student’s t-distribution with 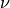 degrees of freedom (given in the argument DF), that is a positive value
degrees of freedom (given in the argument DF), that is a positive value 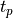 such that the probability
of the absolute value of
such that the probability
of the absolute value of t being greater than 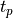 is
is p,
Argument P is of kind stnd and can be a scalar, a vector or a matrix.
This function is parallelized when P is a vector or matrix argument if OPENMP is used.
Note that pinvstudent() does not provide the actual Student’s t inverse.
For q equals to the probability that a Student’s t random variable is less
than 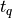 (e.g. the true inverse of the Student’s t distribution function),
that inverse can be obtained with pinvstudent() by the following rules:
(e.g. the true inverse of the Student’s t distribution function),
that inverse can be obtained with pinvstudent() by the following rules:
- for
qin the range[0.0,0.5], call pinvstudent() withp = 2 * qand negate the result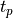 .
. - for
qin the range[0.5,1.0], call pinvstudent() withP = 2 * (1-q).
This function is adapted from [Hill:1970b].
Synopsis:
t = pinvstudent( p , df ) t(:n) = pinvstudent( p(:n) , df ) t(:n,:m) = pinvstudent( p(:n,:m) , df ) t(:n) = pinvstudent( p(:n) , df(:n) ) t(:n,:m) = pinvstudent( p(:n,:m) , df(:n,:m) )
Examples:
-
probq()¶
Purpose:
probq() evaluates the chi-squared distribution function with NDF degrees of freedom from X2 to infinity
if UPPER is true or from zero to X2 if UPPER is false for X2 >= 0.
In other words,
if UPPER =
true: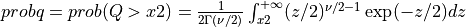
if UPPER =
false: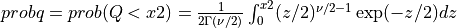
for Q following the chi-squared distribution with 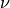 degrees of freedom
degrees of freedom 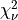 (with
(with 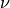 given on input by the argument NDF):
given on input by the argument NDF): 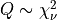 .
.
For NDF <= NDF_MAX, the chi-squared distribution function is integrating by using formulae 26.4.4 and 26.4.5 in [Abramowitz_Stegun:1970], otherwise a normal approximation based on the Wilson-Hilferty transformation is used (see [Abramowitz_Stegun:1970] Formula 26.4.14 and also [Wilson_Hilferty:1931]).
This function works for a scalar, vector or matrix argument X2 and is parallelized when X2 is a vector or matrix argument if OPENMP is used.
Note that probq() works only for integer degrees of freedom. It may be faster than probq2() or
probq3() functions for the default value of NDF_MAX, but it is less accurate.
Synopsis:
p = probq( x2 , ndf , upper , ndf_max=ndf_max ) p(:n) = probq( x2(:n) , ndf , upper , ndf_max=ndf_max ) p(:n,:m) = probq( x2(:n,:m) , ndf , upper , ndf_max=ndf_max ) p(:n) = probq( x2(:n) , ndf(:n) , upper , ndf_max=ndf_max ) p(:n,:m) = probq( x2(:n,:m) , ndf(:n,:m) , upper , ndf_max=ndf_max )
Examples:
-
probq2()¶
Purpose:
probq2() evaluates the chi-squared distribution function with DF degrees of freedom from X2 to infinity
if UPPER is true or from zero to X2 if UPPER is false for X2 >= 0.
In other words,
if UPPER =
true: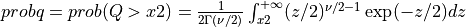
if UPPER =
false: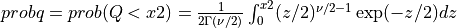
for Q following the chi-squared distribution with 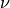 degrees of freedom
degrees of freedom 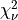 (with
(with 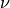 given on input by the argument DF):
given on input by the argument DF): 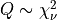 .
.
If DF <= DF_MAX, the chi-squared distribution function is evaluated by integrating the incomplete Gamma integral (see [Abramowitz_Stegun:1970] formulae 6.5.29 and 6.5.32, and [Shea:1988] for more details), otherwise a normal approximation based on the Wilson-Hilferty transformation is used (see [Abramowitz_Stegun:1970] Formula 26.4.14, and also [Wilson_Hilferty:1931]).
This function works for a scalar, vector or matrix argument X2 and is parallelized when X2 is a vector or matrix argument if OPENMP is used.
Note that probq2() works for real degrees of freedom contrary to probq(). It is faster than probq3(),
but it is less accurate.
Synopsis:
p = probq2( x2 , df , upper , df_max=df_max , maxiter=maxiter , failure=failure ) p(:n) = probq2( x2(:n) , df , upper , df_max=df_max , maxiter=maxiter , failure=failure ) p(:n,:m) = probq2( x2(:n,:m) , df , upper , df_max=df_max , maxiter=maxiter , failure=failure ) p(:n) = probq2( x2(:n) , df(:n) , upper , df_max=df_max , maxiter=maxiter , failure=failure ) p(:n,:m) = probq2( x2(:n,:m) , df(:n,:m) , upper , df_max=df_max , maxiter=maxiter , failure=failure )
Examples:
-
probq3()¶
Purpose:
probq3() evaluates the chi-squared distribution function with DF degrees of freedom from X2 to infinity
if UPPER is true or from zero to X2 if UPPER is false for X2 >= 0.
In other words,
if UPPER =
true: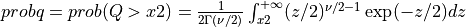
if UPPER =
false: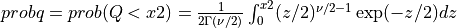
for Q following the chi-squared distribution with 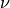 degrees of freedom
degrees of freedom 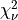 (with
(with 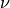 given on input by the argument DF):
given on input by the argument DF): 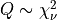 .
.
If DF <= DF_MAX, the chi-squared distribution function is evaluated by integrating the incomplete Gamma integral (see [Abramowitz_Stegun:1970] formulae 6.5.29 and 6.5.31, and [Shea:1988] for more details), otherwise a normal approximation based on the Wilson-Hilferty transformation is used (see [Abramowitz_Stegun:1970] Formula 26.4.14, and also [Wilson_Hilferty:1931]).
This function works for a scalar, vector or matrix argument X2 and is parallelized when X2 is a vector or matrix argument if OPENMP is used.
Note that probq3() works for real degrees of freedom contrary to probq(). It is slower than probq() or probq2(),
but it is more accurate.
Synopsis:
p = probq3( x2 , df , upper , df_max=df_max , acu=acu , maxiter=maxiter , failure=failure ) p(:n) = probq3( x2(:n) , df , upper , df_max=df_max , acu=acu , maxiter=maxiter , failure=failure ) p(:n,:m) = probq3( x2(:n,:m) , df , upper , df_max=df_max , acu=acu , maxiter=maxiter , failure=failure ) p(:n) = probq3( x2(:n) , df(:n) , upper , df_max=df_max , acu=acu , maxiter=maxiter , failure=failure ) p(:n,:m) = probq3( x2(:n,:m) , df(:n,:m) , upper , df_max=df_max , acu=acu , maxiter=maxiter , failure=failure )
Examples:
-
pinvq()¶
Purpose:
pinvq() evaluates the inverse of the chi-squared distribution function with NDF degrees of freedom for the argument P,
with 0 < P < 1 (P can be a scalar, a vector or a matrix). pinvq() returns the quantile 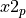 of
the chi-squared distribution with
of
the chi-squared distribution with 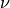 degrees of freedom (given in the argument NDF) corresponding to a given lower
tail area of
degrees of freedom (given in the argument NDF) corresponding to a given lower
tail area of p.
In other words, pinvq() outputs a chi-squared value 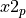 such that a random variable, distributed as chi-squared
with
such that a random variable, distributed as chi-squared
with 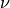 degrees of freedom will be less than
degrees of freedom will be less than 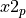 with probability
with probability p.
This function is parallelized when P is a vector or matrix argument if OPENMP is used.
pinvq() is fast, but not very accurate, especially for small degrees of freedom,
e.g. for NDF < 10 or 20. If high accuracy is desired, function pinvq2() must be used
instead. Moreover, pinvq() works only for integer degrees of freedom NDF.
This function is adapted from [Goldstein:1973]
Synopsis:
x2 = pinvq( p , ndf ) x2(:n) = pinvq( p(:n) , ndf ) x2(:n,:m) = pinvq( p(:n,:m) , ndf ) x2(:n) = pinvq( p(:n) , ndf(:n) ) x2(:n,:m) = pinvq( p(:n,:m) , ndf(:n,:m) )
Examples:
-
pinvq2()¶
Purpose:
pinvq2() evaluates the inverse of the chi-squared distribution function with DF degrees of freedom for the argument P,
with 0 < P < 1 (P can be a scalar, a vector or a matrix). pinvq2() returns the quantile 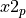 of
the chi-squared distribution with
of
the chi-squared distribution with 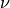 degrees of freedom (given in the argument DF) corresponding to a given lower
tail area of
degrees of freedom (given in the argument DF) corresponding to a given lower
tail area of p
In other words, pinvq2() outputs a chi-squared value 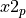 such that a random variable, distributed as chi-squared
with
such that a random variable, distributed as chi-squared
with 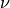 degrees of freedom will be less than
degrees of freedom will be less than 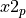 with probability
with probability p.
This function is parallelized when P is a vector or matrix argument if OPENMP is used.
pinvq2() is both more general (here the number of degrees of freedom, DF,
is not necessarily an integer) and more accurate (here the quantile 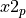 may be calculated
as exactly as the computer allows with the parameter PREC) than
may be calculated
as exactly as the computer allows with the parameter PREC) than pinvq() function.
This function is adapted from [Best_Roberts:1975] and [Shea:1991]
Synopsis:
x2 = pinvq2( p , df , prec=prec , acu=acu , maxiter=maxiter ) x2(:n) = pinvq2( p(:n) , df , prec=prec , acu=acu , maxiter=maxiter ) x2(:n,:m) = pinvq2( p(:n,:m) , df , prec=prec , acu=acu , maxiter=maxiter ) x2(:n) = pinvq2( p(:n) , df(:n) , prec=prec , acu=acu , maxiter=maxiter ) x2(:n,:m) = pinvq2( p(:n,:m) , df(:n,:m) , prec=prec , acu=acu , maxiter=maxiter )
Examples:
-
probf()¶
Purpose:
probf() evaluates the F-distribution function with degrees of freedom NDF1 and NDF2
from F to infinity if UPPER is true or from zero to F if UPPER is false for a
given input argument F >= 0.
If 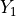 and
and 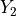 are chi-squared deviates with
are chi-squared deviates with 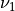 and
and 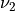 degrees of
freedom, respectively, then the ratio,
degrees of
freedom, respectively, then the ratio,
has an F-distribution 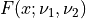 .
.
Thus [Walck:2007],
if UPPER =
true: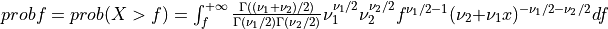
if UPPER =
false: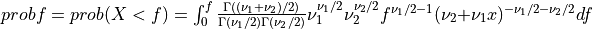
where 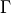 is the usual Gamma function and
is the usual Gamma function and X follows an F-distribution with 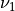 and
and 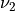 degrees
of freedom (given on input by the real arguments DF1 and DF2, respectively):
degrees
of freedom (given on input by the real arguments DF1 and DF2, respectively): 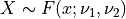 .
.
Argument F can be a scalar, a vector or a matrix.
This function is parallelized when F is a vector or matrix argument if OPENMP is used.
probf() accepts only integer values of degree of freedom and uses a normal approximation. See formula 2.24a in [Peizer_Pratt:1968] for more details. This normal approximation is not accurate for small values of degrees of freedom.
Synopsis:
p = probf( f , ndf1 , ndf2 , upper ) p(:n) = probf( f(:n) , ndf1 , ndf2 , upper ) p(:n,:m) = probf( f(:n,:m) , ndf1 , ndf2 , upper ) p(:n) = probf( f(:n) , ndf1(:n) , ndf2(:n) , upper ) p(:n,:m) = probf( f(:n,:m) , ndf1(:n,:m) , ndf2(:n,:m) , upper )
-
probf2()¶
Purpose:
probf2() evaluates the F-distribution function with degrees of freedom DF1 and DF2
from F to infinity if UPPER is true or from zero to F if UPPER is false for a
given input argument F greater than or equal to zero.
If 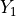 and
and 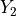 are chi-squared deviates with
are chi-squared deviates with 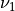 and
and 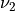 degrees of
freedom, respectively, then the ratio,
degrees of
freedom, respectively, then the ratio,
has an F-distribution 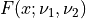 .
.
Thus [Walck:2007],
if UPPER =
true: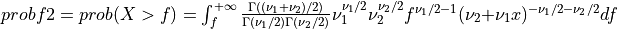
if UPPER =
false: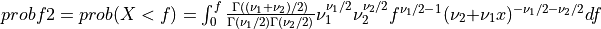
where 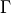 is the usual Gamma function and
is the usual Gamma function and X follows an F-distribution with 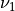 and
and 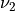 degrees
of freedom (given on input by the real arguments DF1 and DF2, respectively):
degrees
of freedom (given on input by the real arguments DF1 and DF2, respectively): 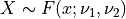 .
.
Argument F can be a scalar, a vector or a matrix.
This function is parallelized when F is a vector or matrix argument if OPENMP is used.
probf2() accepts real values of degree of freedom and, actually, invokes the Beta distribution
function probbeta() for computing the probability associated with the F-distribution [Walck:2007].
Thus, probf2() is much more accurate than probf(), but it is slower.
Synopsis:
p = probf2( f , df1 , df2 , upper , beta=beta , acu=acu , maxiter=maxiter , failure=failure ) p(:n) = probf2( f(:n) , df1 , df2 , upper , beta=beta , acu=acu , maxiter=maxiter , failure=failure ) p(:n,:m) = probf2( f(:n,:m) , df1 , df2 , upper , beta=beta , acu=acu , maxiter=maxiter , failure=failure ) p(:n) = probf2( f(:n) , df1(:n) , df2(:n) , upper , beta=beta , acu=acu , maxiter=maxiter , failure=failure ) p(:n,:m) = probf2( f(:n,:m) , df1(:n,:m) , df2(:n,:m) , upper , beta=beta , acu=acu , maxiter=maxiter , failure=failure )
-
pinvf2()¶
Purpose:
pinvf2() evaluates the inverse F probability distribution function with degrees of freedom
DF1 and DF2 (integer or fractional degrees of freedom > 0.2), for the given argument P with
0 < P < 1.
Thus, pinvf2() returns the quantile 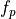 of the F-distribution
of the F-distribution
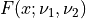 (where
(where 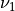 and
and 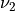 are given in DF1 and DF2,
respectively) corresponding to a given lower tail area of
are given in DF1 and DF2,
respectively) corresponding to a given lower tail area of p
In other words, pinvf2() outputs a F value  such that a random variable, distributed as a F-distribution
with
such that a random variable, distributed as a F-distribution
with 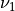 and
and 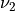 degrees of freedom will be less than
degrees of freedom will be less than 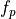 with probability
with probability p.
where 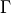 is the usual Gamma function.
is the usual Gamma function.
This function actually invoked the inverse BETA distribution function pinvbeta()
for computing the value 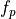 associated with the probability P.
associated with the probability P.
P can be a scalar, a vector or a matrix and this function is parallelized when P is a vector or matrix argument if OPENMP is used.
This function is not very accurate for small values of DF1 and/or DF2 (e.g. less than 1 ).
Synopsis:
f = pinvf2( p , df1 , df2 , beta=beta , acu=acu , maxiter=maxiter )
-
probbinom()¶
Purpose:
probbinom() evaluates the cumulative binomial probability distribution function for a positive real
argument PROB (with 0 <= PROB <= 1), a strictly positive integer N and a positive integer
K less than or equal to N.
probbinom() computes the probability that an event occurring with probability PROB per trial, will occur:
K or more times in N independent trials if UPPER is
true: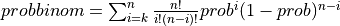
K or less times in N independent trials if UPPER is
false: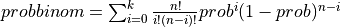
This probability is estimated with the help of the incomplete Beta function, as computed by
function probbeta(), and the optional arguments BETA, ACU, MAXITER and FAILURE are passed
directly to probbeta() if these arguments are present.
Synopsis:
p = probbinom( prob , n , k , upper , beta=beta , acu=acu , maxiter=maxiter , failure=failure )
-
rangen()¶
Purpose:
rangen() evaluates the probability that the normal range (e.g. the standardized difference between
the maximum and the minimum on a sample) will be less than X (X > 0) for a normal sample
of size N.
For algorithm and details, see [Barnard:1978]
Synopsis:
p = rangen( x , n ) p(:n) = rangen( x(:n) , n )